 Startseite
| Programm-Archiv
| Lektion:
Ableitungen
|
Unserer Vorläufer
| Kontakt, Datenschutz
Startseite
| Programm-Archiv
| Lektion:
Ableitungen
|
Unserer Vorläufer
| Kontakt, Datenschutz
Wir bewältigen unseren Alltag
fast ohne das geringste Verständnis der Welt.
Carl Sagan
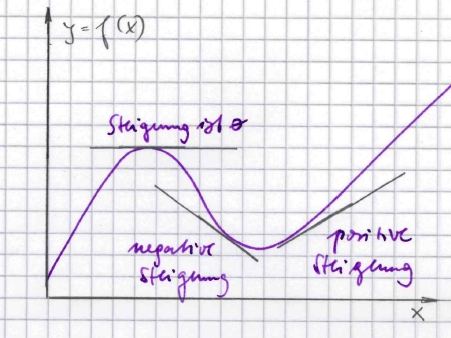
Wenn mann eine typische Kurve anschaut, dann hat diese flachere und steilere Abschnitte. Man kann ein Lineal anlegen und diese Steilheit mit einer gewissen Genauigkeit messen. Diese Steilheit bezeichnet man als Anstieg, abgekürzt wird y' oder f
'(x) geschrieben.
Man kann diesen Anstieg auch näherungsweise ausrechnen.
Es gilt nämlich
f '(x) ≈ Δy / Δx,
wobei
Δx und Δy kleine Änderungen in der Nähe des Punktes sind, für den man den
Anstieg benötigt.
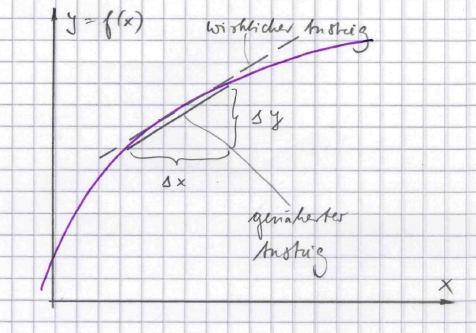
Je kleiner man Δx und Δy macht, desto näher kommt man dem
wirklichen Anstieg. Man kann somit diese Anstiege auch dann berechnen, wenn es
sich um gar keine formelmäßige Funktion, sondern z.B. um Messwerte handelt.
Man muss dabei immer einen Kompromiss finden zwischen der mathematischen
Genauigkeit (Δx und Δy sind klein) und der messtechnischen Genauigkeit
(Δx und Δy sollten deutliche größer sein als die Messfehler).
Eine Ableitung kann man wieder ableiten, diese zweite Ableitung bezeichnet man dann als y'' bzw. f ''(y). Anschaulich ist das die Krümmung der Kurve. Noch höhere Ableitungen wie f '''(x) haben keine anschauliche Bedeutung mehr.
Wenn man höhere Ableitungen aus den Ergebnissen von numerischen Näherungsverfahren bestimmen will, dann muss man sich mit diesen Näherungen viel Mühe geben. Aus einer Messkurve lässt sich höchstens noch die zweite Ableitung mit einiger Genauigkeit bestimmen - hier kann man die Genauigkeit nicht beliebig erhöhen.
Für die formelmäßig gegebenen Zusammenhänge lassen sich Ableitungen mathematisch bestimmen, führen also wieder zu Formeln. Diese findet man im Schul-Tafelwerk. Ich benutze immer einen Online-Ableitungsrechner [1]. Der macht weniger Fehler als ich.
Die Webseite Sun or Moon rise set [2] gestattet es, den Sonnenaufgang
und -untergang für amerikanische Städte zu berechnen. Ich habe Seattle
ausgewählt, weil es genügend weit nördlich liegt und dabei stellvertretend für
den deutschen Sprachraum stehen kann. Man erhält die im Anhang dargestellte
Tabelle.
Mit Hilfe eines kleinen Programms habe ich die Taglängen
ausgerechnet:
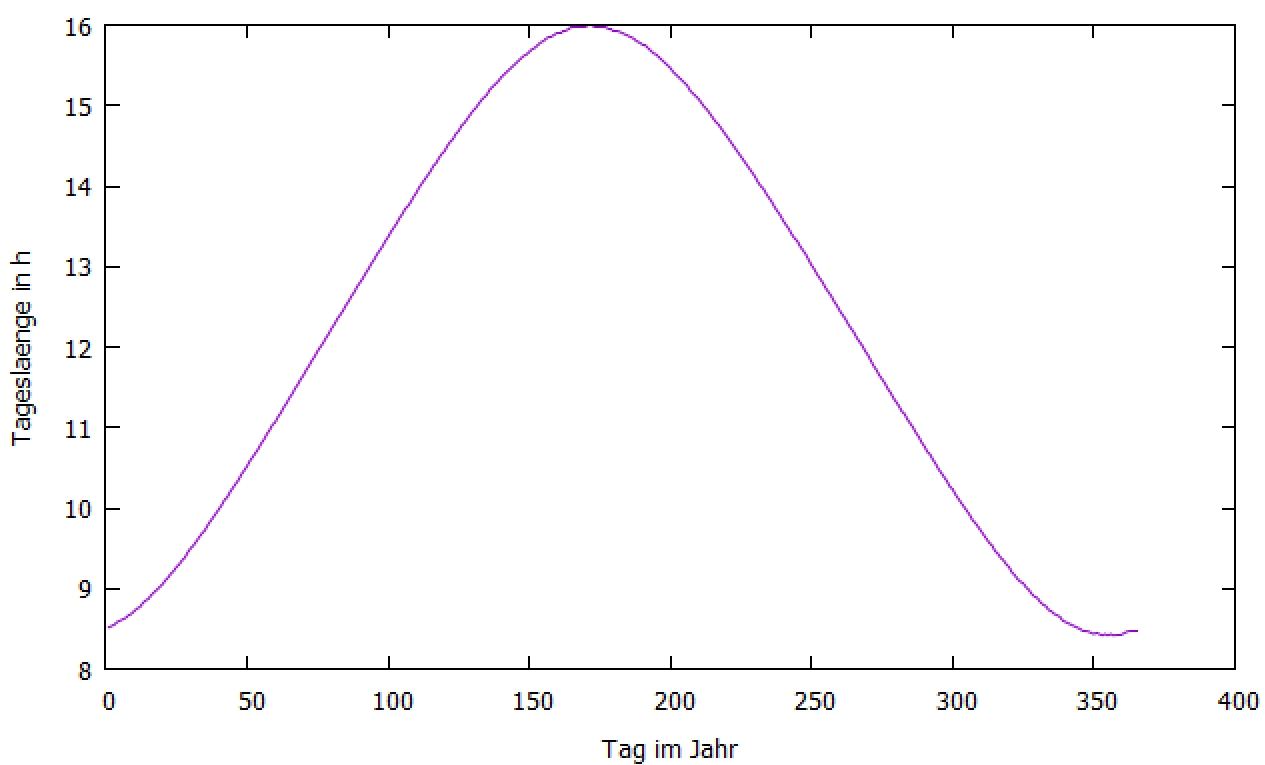
Es ist nun interessant zu wissen, wie sich die Tageslänge im Verlauf der
Jahreszeiten ändert. Dazu kann man die Differenzen von Tag zu Tag benutzen.
Das ist genaugenommen eine Ableitung, und zwar eine ungenaue, eine
"einseitige". Besser ist es, für die Änderung der Tageslänge den Mittelwert
der veränderung vom vorangegangen und zum nächsten Tag zu benutzen
VT = [ LT(heute) -LT(gestern) + LT(morgen) -LT(heute) ] /2
oder kürzer
VT(heute) = [ LT(morgen) - LT(gestern) ] /2
Hierbei ist LT die Tageslänge und VT die tägliche
Veränderung.
# Tageslängen einlesen
fIn = open("tageslaenge.txt")
# Tageslängen erst mal irgendwie setzen
tag=0
gestern=0
heute=0
morgen=0
# Veränderungen berechnen
for line in fIn:
# eine Tag nachrutschen
gestern=heute
heute=morgen
# Zeile in Wörter teilen
arr = line.split(" ")
# die beiden Werte auslesen
morgen=float(arr[1])
tagesnrMorgen=int(arr[0])
# den Anstieg berechnen
print(tagesnrMorgen-1,60*(morgen-gestern)/2.0)
Damit das Programm kurz bleibt, habe ich mich nicht darum gekümmert, dass
für die ersten beiden Tage falsche Ausgaben erzeugt werden.
Grafisch
dargestellt erhält man
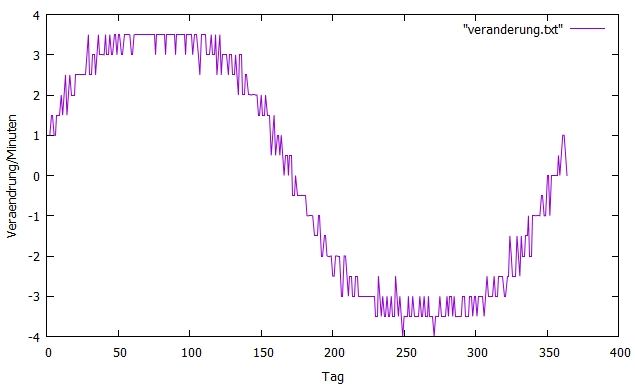
Man sieht, dass die Kurve "zackelig" ist. Dies lieg daran, dass die
Veränderung der Tageslänge nur auf die ganze Minute gegeben ist. Bei der
Bildung der Ableitung ziehen wir zwei fast gleich große Zahlen voneinander
ab und erhöhen damit das "Rauschen".
Dennoch enthält diese Kurve
wichtige Aussagen:
Man kann nur auch die Frage stellen, zu welchen Jahreszeiten die Veränderung der Tageslänge selbst stark variabel ist. Man kann dies wieder durch Differenzenbildung errechnen, diesmal aber aus den schon zackeligen täglichen Veränderungen. Das Programm muss dafür nur ganz wenig verändert werden (anderer Dateiname). Das Ergebnis:
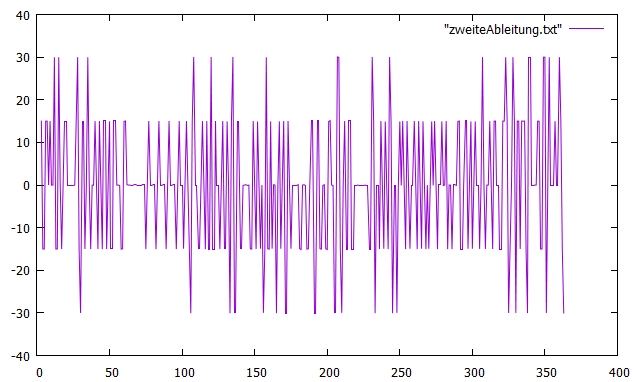
Nur noch Gezackel - kaum noch etwas zu erkennen. Wie ich oben schon
schrieb: Um eine zweite Ableitung aus Messwerten zu berechnen, muss man sich
einige Mühe machen. Entweder die Messwerte mit höherer Genauigkeit bestimmen
(was nicht immer geht), oder die erste Ableitung vor der Weiterverwendung
glätten. Wer Sonnenflecken-Relativzahlen bestimmt, steht vor ganz
ähnlichen Problemen.
Die Funktion
ex ist die
Exponentialfunktion. Mit ihr wird das in der Natur häufig vorkommende
unbeschränkte Wachstum beschrieben. Es gilt:
f '( ex) =
ex
Damit haben alle weitere Ableitungen auch den Wert
ex.
Es gilt
f '(sin(x)) = cos(x)
f ''(sin(x)) = -sin(x)
f ''(sin(x)) =
-cos(x)
f '''(sin(x)) = sin(x)
Nach vier Mal ist "die Runde rum".
[1] www.ableitungsrechner.net
[2] aa.usno.navy.mil/data/docs/RS_OneYear.php
(Uwe Pilz, Dezember 2018)
=====================================
o , o , SEATTLE, WASHINGTON Astronomical Applications Dept.
Location: W122 20, N47 38 Rise and Set for the Sun for 2018 U. S. Naval Observatory
Washington, DC 20392-5420
Pacific Standard Time
Jan. Feb. Mar. Apr. May June July Aug. Sept. Oct. Nov. Dec.
Day Rise Set Rise Set Rise Set Rise Set Rise Set Rise Set Rise Set Rise Set Rise Set Rise Set Rise Set Rise Set
h m h m h m h m h m h m h m h m h m h m h m h m h m h m h m h m h m h m h m h m h m h m h m h m
01 0758 1629 0736 1711 0650 1754 0548 1839 0452 1922 0416 1959 0416 2011 0447 1944 0528 1849 0609 1748 0654 1652 0737 1620
02 0758 1630 0734 1712 0648 1756 0546 1841 0450 1923 0415 2000 0416 2010 0448 1942 0529 1848 0610 1746 0655 1650 0738 1619
03 0758 1631 0733 1714 0646 1757 0544 1842 0449 1924 0414 2001 0417 2010 0450 1941 0531 1846 0611 1744 0657 1648 0739 1619
04 0757 1632 0732 1715 0644 1759 0542 1844 0447 1926 0414 2002 0418 2010 0451 1939 0532 1844 0613 1742 0658 1647 0740 1619
05 0757 1633 0730 1717 0642 1800 0540 1845 0446 1927 0413 2003 0418 2009 0452 1938 0533 1842 0614 1740 0700 1646 0742 1618
06 0757 1634 0729 1719 0640 1802 0538 1847 0444 1929 0413 2004 0419 2009 0453 1936 0535 1840 0616 1738 0701 1644 0743 1618
07 0757 1635 0727 1720 0638 1803 0536 1848 0443 1930 0413 2004 0420 2008 0455 1935 0536 1837 0617 1736 0703 1643 0744 1618
08 0756 1636 0726 1722 0636 1805 0534 1849 0441 1931 0412 2005 0421 2008 0456 1933 0537 1835 0618 1734 0704 1641 0745 1618
09 0756 1637 0724 1723 0634 1806 0532 1851 0440 1933 0412 2006 0422 2007 0457 1931 0539 1833 0620 1732 0706 1640 0746 1618
10 0756 1639 0723 1725 0632 1808 0530 1852 0438 1934 0412 2006 0422 2007 0459 1930 0540 1831 0621 1731 0707 1639 0747 1618
11 0755 1640 0721 1727 0630 1809 0528 1854 0437 1935 0411 2007 0423 2006 0500 1928 0541 1829 0623 1729 0709 1637 0748 1618
12 0755 1641 0720 1728 0628 1811 0526 1855 0436 1937 0411 2007 0424 2005 0501 1926 0543 1827 0624 1727 0710 1636 0749 1618
13 0754 1643 0718 1730 0626 1812 0524 1856 0434 1938 0411 2008 0425 2004 0503 1925 0544 1825 0625 1725 0712 1635 0749 1618
14 0753 1644 0716 1731 0624 1814 0522 1858 0433 1939 0411 2009 0426 2004 0504 1923 0545 1823 0627 1723 0713 1634 0750 1618
15 0753 1645 0715 1733 0622 1815 0520 1859 0432 1940 0411 2009 0427 2003 0505 1921 0547 1821 0628 1721 0715 1633 0751 1618
16 0752 1647 0713 1734 0620 1817 0518 1901 0430 1942 0411 2009 0428 2002 0507 1920 0548 1819 0630 1719 0716 1632 0752 1618
17 0751 1648 0711 1736 0618 1818 0517 1902 0429 1943 0411 2010 0429 2001 0508 1918 0550 1817 0631 1717 0718 1630 0752 1619
18 0751 1650 0710 1738 0616 1819 0515 1903 0428 1944 0411 2010 0430 2000 0509 1916 0551 1815 0633 1715 0719 1629 0753 1619
19 0750 1651 0708 1739 0614 1821 0513 1905 0427 1945 0411 2010 0431 1959 0511 1914 0552 1813 0634 1714 0721 1628 0754 1619
20 0749 1652 0706 1741 0612 1822 0511 1906 0426 1947 0411 2011 0433 1958 0512 1912 0554 1811 0636 1712 0722 1627 0754 1620
21 0748 1654 0704 1742 0610 1824 0509 1908 0425 1948 0411 2011 0434 1957 0513 1911 0555 1809 0637 1710 0723 1627 0755 1620
22 0747 1655 0703 1744 0608 1825 0507 1909 0424 1949 0412 2011 0435 1956 0515 1909 0556 1807 0639 1708 0725 1626 0755 1621
23 0746 1657 0701 1745 0606 1827 0506 1911 0423 1950 0412 2011 0436 1955 0516 1907 0558 1805 0640 1706 0726 1625 0756 1621
24 0745 1658 0659 1747 0604 1828 0504 1912 0422 1951 0412 2011 0437 1954 0517 1905 0559 1803 0642 1705 0728 1624 0756 1622
25 0744 1700 0657 1748 0602 1829 0502 1913 0421 1952 0413 2011 0438 1953 0519 1903 0600 1801 0643 1703 0729 1623 0757 1623
26 0743 1701 0655 1750 0600 1831 0500 1915 0420 1953 0413 2011 0440 1951 0520 1901 0602 1759 0645 1701 0730 1623 0757 1623
27 0742 1703 0653 1751 0558 1832 0459 1916 0419 1954 0414 2011 0441 1950 0521 1859 0603 1757 0646 1700 0732 1622 0757 1624
28 0741 1704 0651 1753 0556 1834 0457 1918 0418 1955 0414 2011 0442 1949 0523 1857 0604 1754 0648 1658 0733 1621 0757 1625
29 0739 1706 0554 1835 0455 1919 0418 1956 0415 2011 0443 1948 0524 1855 0606 1752 0649 1656 0734 1621 0757 1626
30 0738 1708 0552 1837 0454 1920 0417 1957 0415 2011 0444 1946 0525 1853 0607 1750 0651 1655 0736 1620 0758 1627
31 0737 1709 0550 1838 0416 1958 0446 1945 0527 1851 0652 1653 0758 1627
Add one hour for daylight time, if and when in use.
1 8.51667
2 8.53333
3 8.55
4 8.58333
5 8.6
6 8.61667
7 8.63333
8 8.66667
9 8.68333
10 8.71667
11 8.75
12 8.76667
13 8.81667
14 8.85
15 8.86667
16 8.91667
17 8.95
18 8.98333
19 9.01667
20 9.05
21 9.1
22 9.13333
23 9.18333
24 9.21667
25 9.26667
26 9.3
27 9.35
28 9.38333
29 9.45
30 9.5
31 9.53333
32 9.58333
33 9.63333
34 9.68333
35 9.71667
36 9.78333
37 9.83333
38 9.88333
39 9.93333
40 9.98333
41 10.0333
42 10.1
43 10.1333
44 10.2
45 10.25
46 10.3
47 10.35
48 10.4167
49 10.4667
50 10.5167
51 10.5833
52 10.6333
53 10.6833
54 10.7333
55 10.8
56 10.85
57 10.9167
58 10.9667
59 11.0333
60 11.0667
61 11.1333
62 11.1833
63 11.25
64 11.3
65 11.3667
66 11.4167
67 11.4833
68 11.5333
69 11.6
70 11.65
71 11.7167
72 11.7667
73 11.8333
74 11.8833
75 11.95
76 12
77 12.05
78 12.1167
79 12.1667
80 12.2333
81 12.2833
82 12.35
83 12.4
84 12.45
85 12.5167
86 12.5667
87 12.6333
88 12.6833
89 12.75
90 12.8
91 12.85
92 12.9167
93 12.9667
94 13.0333
95 13.0833
96 13.15
97 13.2
98 13.25
99 13.3167
100 13.3667
101 13.4333
102 13.4833
103 13.5333
104 13.6
105 13.65
106 13.7167
107 13.75
108 13.8
109 13.8667
110 13.9167
111 13.9833
112 14.0333
113 14.0833
114 14.1333
115 14.1833
116 14.25
117 14.2833
118 14.35
119 14.4
120 14.4333
121 14.5
122 14.55
123 14.5833
124 14.65
125 14.6833
126 14.75
127 14.7833
128 14.8333
129 14.8833
130 14.9333
131 14.9667
132 15.0167
133 15.0667
134 15.1
135 15.1333
136 15.2
137 15.2333
138 15.2667
139 15.3
140 15.35
141 15.3833
142 15.4167
143 15.45
144 15.4833
145 15.5167
146 15.55
147 15.5833
148 15.6167
149 15.6333
150 15.6667
151 15.7
152 15.7167
153 15.75
154 15.7833
155 15.8
156 15.8333
157 15.85
158 15.85
159 15.8833
160 15.9
161 15.9
162 15.9333
163 15.9333
164 15.95
165 15.9667
166 15.9667
167 15.9667
168 15.9833
169 15.9833
170 15.9833
171 16
172 16
173 15.9833
174 15.9833
175 15.9833
176 15.9667
177 15.9667
178 15.95
179 15.95
180 15.9333
181 15.9333
182 15.9167
183 15.9
184 15.8833
185 15.8667
186 15.85
187 15.8333
188 15.8
189 15.7833
190 15.75
191 15.75
192 15.7167
193 15.6833
194 15.65
195 15.6333
196 15.6
197 15.5667
198 15.5333
199 15.5
200 15.4667
201 15.4167
202 15.3833
203 15.35
204 15.3167
205 15.2833
206 15.25
207 15.1833
208 15.15
209 15.1167
210 15.0833
211 15.0333
212 14.9833
213 14.95
214 14.9
215 14.85
216 14.8
217 14.7667
218 14.7167
219 14.6667
220 14.6167
221 14.5667
222 14.5167
223 14.4667
224 14.4167
225 14.3667
226 14.3167
227 14.2667
228 14.2167
229 14.1667
230 14.1167
231 14.05
232 14
233 13.9667
234 13.9
235 13.85
236 13.8
237 13.7333
238 13.6833
239 13.6333
240 13.5667
241 13.5167
242 13.4667
243 13.4
244 13.35
245 13.3167
246 13.25
247 13.2
248 13.15
249 13.0833
250 13.0167
251 12.9667
252 12.9
253 12.85
254 12.8
255 12.7333
256 12.6833
257 12.6333
258 12.5667
259 12.5167
260 12.45
261 12.4
262 12.35
263 12.2833
264 12.2333
265 12.1833
266 12.1167
267 12.0667
268 12.0167
269 11.95
270 11.9
271 11.8333
272 11.7667
273 11.7167
274 11.65
275 11.6
276 11.55
277 11.4833
278 11.4333
279 11.3667
280 11.3167
281 11.2667
282 11.2
283 11.1667
284 11.1
285 11.05
286 11
287 10.9333
288 10.8833
289 10.8167
290 10.7667
291 10.7
292 10.6667
293 10.6
294 10.55
295 10.4833
296 10.4333
297 10.3833
298 10.3333
299 10.2667
300 10.2333
301 10.1667
302 10.1167
303 10.0667
304 10.0167
305 9.96667
306 9.91667
307 9.85
308 9.81667
309 9.76667
310 9.71667
311 9.66667
312 9.61667
313 9.56667
314 9.53333
315 9.46667
316 9.43333
317 9.38333
318 9.35
319 9.3
320 9.26667
321 9.2
322 9.16667
323 9.11667
324 9.08333
325 9.06667
326 9.01667
327 8.98333
328 8.93333
329 8.9
330 8.88333
331 8.83333
332 8.8
333 8.78333
334 8.73333
335 8.71667
336 8.68333
337 8.66667
338 8.65
339 8.6
340 8.58333
341 8.56667
342 8.55
343 8.53333
344 8.51667
345 8.5
346 8.48333
347 8.48333
348 8.46667
349 8.45
350 8.43333
351 8.45
352 8.43333
353 8.41667
354 8.43333
355 8.41667
356 8.43333
357 8.41667
358 8.43333
359 8.43333
360 8.43333
361 8.45
362 8.46667
363 8.48333
364 8.48333
365 8.48333