Das Halbierungsverfahren zur Bestimmung von Nullstellen

Das Halbierungsverfahren ist eine leicht zu programmierende Methode zur Suche einer Nullstelle. Voraussetzung ist, dass man zwei Argumente (x-Werte) findet, zwischen denen genau eine Nullstelle liegt. Beim großen Diagramm ist das gegeben, bei den beiden Beispielen am Rand ist das Verfahren nicht einsetzbar.

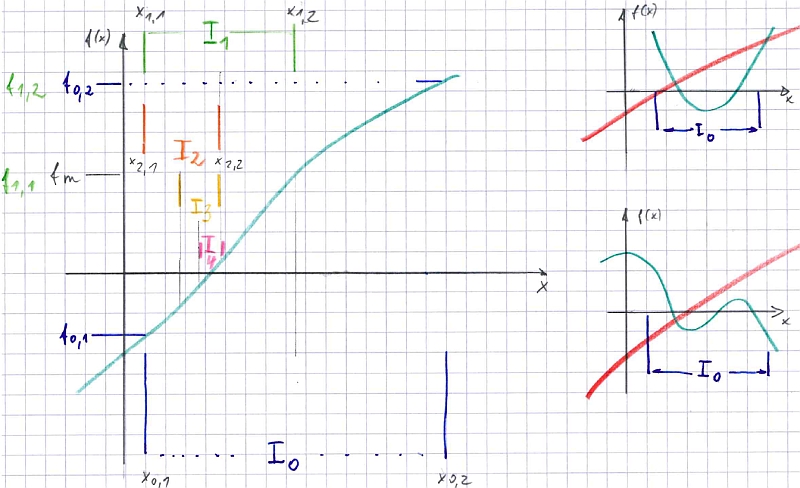
Das Anfangsintervall I₀ wird durch die beiden x-Werte x_0,1 und x_0,2 begrenzt. In einem Initialisierungsschritt werden hierzu die beiden Funktionswerte f_0,1 und f_0,2 berechnet. Einer der beiden Werte ist positiv und eine anderer negativ.

Das Halbierungsverfahren grenzt nun die Nullstelle schrittweise so ein, dass sich die Intervallbreite in jedem Schritt halbiert. Dazu wird der Funktionswert in der Mitte des Intervalls bestimmt. Für den ersten Schritt ist dieser als f_m gekennzeichnet. Wenn dieser Funktionswert negativ ist, dann wird die "negative Grenze" zur wahren Nullstelle hin versetzt, wenn er positiv ist, "positive Grenze". Die beiden Funktionswerte (z.B. f_1,1 und f_1,2 im ersten Schritt) sind schon bekannt und müssen nicht erneut berechnet werden. Dieses Verfahren wird so lange fortgesetzt, bis die gewünschte Genauigkeit erreicht ist. Als Faustregel gilt, dass 10 Halbierungsschritte die Intervallbreite auf 1/1000 verringern.

Im Beispiel sind die ersten vier Halbierungsschritte eigezeichnet. Im ersten Schritt wird die rechte Grenze versetzt, weil der Funktionswert f_m = f_1,1 positiv ist, und den ebenso positiven f_0,2 ersetzt. Im zweiten Schritt wird wieder die rechte Grenze versetzt, in den beiden nächsten die linke. Das Intervall wurde dadurch auf 1/16 verkleinert.

==
Uwe Pilz, April 2020.