Interpolation mit Polynomen

Was ist ein Polynom?

Ein Polynom ist eine Funktion, bei der ganzzahlige Koeffizienten von x vorkommen, also in etwa

y = a · x² +b · x +c

Die größte Potenz heißt Grad, das Beispiel ist ein Polynom 2. Grades. a, b und c heißen die Koeffizienten des Polynoms. Solche Polynome lassen sich leicht berechnen, sie können per Formel integriert und differenziert werden. Aus diesem Grund werden sie in einer Reihe von mathematisch-numerischen Verfahren eingesetzt.
Die Mathematiker haben nachgewiesen, dass sich durch eine Anzahl vorgegebener Punkte (z.B. Messwerte) stets ein Polynom legen lässt, was einen Grad geringer ist. Durch drei Punkte lässt sich also immer ein Polynom 2. Grades (eine Parabel) legen. Dieses Polynom kann man dazu benutzen, Zwischenwerte auszurechnen, deshalb heißt es Interpolationspolynom. Theoretisch gilt: Je mehr Messwerte einbezogen werden, desto genauer ist die Annäherung in der Mitte des Intervalls. Praktisch kann es aber seltsame Effekte geben, die ich hier auch bespreche.

Wie berechnet man die Koeffizienten?

Es gibt verschiedene Formeln, die Koeffizienten zu bestimmen: Nach Langrange, nach Newton, nach Gauß. Sie wurde entworfen, um die manuelle Rechenarbeit zu erleichtern – in früheren Zeiten wurde dies ja alles mit Stift und Papier ausgeführt. Ich benutze hier den direkten Polynomansatz, der leicht verständlich ist und zu einem Resultat führt, was man sehr allgemeingültig einsetzen kann: Nicht nur zum Interpolieren, sondern auch zum Integrieren oder Differenzieren.
Asugangspunkt der Berechnung ist ein sogenannte Ansatz. Das heiß man nimmt an, dass die Punkte zu einem Polynom gehören, was man aber noch nicht kennt. Für ein Polynom 2. Grades ergeben sich dann durch die drei Punkte (Messwerte) drei Gleichungen, welche zur Bestimmung der Koeffizienten a, b und c dienen können.

y₁ = a · x²₁ +b · x₁ +c
y₂ = a · x²₂ +b · x₂ +c
y₃ = a · x²₃ +b · x₃ +c

Diese Gleichungen bilden ein Lineares Gleichungssystem, mit welchem man diese Koeffizienten berechnen kann. Ich gebe hier ein kleines Python-Programm an, welches Polynome verschiedenen Grades ausrechnet. Als "Messwerte" habe ich die sog. Runge-Funktion benutzt, welche zeigt, dass Polynome höheren Grades zu "seltsamen Effekten" führen können. Der Vorteil ist jedenfalls, dass ich so viele Werte berechnen kann, wie für das Polynom benötigt werden. Ihr könnt also mit einem Polynom 100. Grades experimentieren!


def gauss(n, m): 
    for i in range (n): 
        max=0; k=0
        for j in range(i,n): 
            if abs(m[j][i])>max:
                   max=abs(m[j][i]); k=j
        for j in range(n+1):
            h=m[i][j]
            m[i][j]=m[k][j]
            m[k][j]=h
        for j in range (n): 
            f=m[j][i]/m[i][i]
            for k in range(i,n+1): 
                if (i!=j):
                    m[j][k]=m[j][k]-f*m[i][k]

# Hauptprogramm
n=11 # Grad des Polynoms
n=n+1 # Gleichungssystem hat eine Dimension mehr
# leere Matrix
m = [[0 for i in range(n+1)] for j in range(n)]
# Vektoren für die "Messwerte"
xm = [0 for i in range(n)]
ym = [0 for i in range(n)]
# Runge-Funktion einfüllen
x=-5
for i in range (n):
    xm[i]=x;
    ym[i]=1/(1+x*x)
    x=x+10/(n-1)
#LGS aufbauen
for i in range (n):
    xPot=1
    for j in range (n):
        m[i][j]=xPot
        xPot=xPot*xm[i]
    m[i][n]=ym[i]
# LGS lösen
gauss(n,m)
# Ergebnisvektor
a = [0 for i in range(n)]
for i in range (n):
    a[i]=m[i][n]/m[i][i]
# Polynom in feinen Stufen ausgeben
x=-5
for i in range(100):
    xPot=1
    y=0
    for j in range (n):
        y=y+a[j]*xPot
        xPot=xPot*x
    print(x,y)
    x=x+0.1

Ein paar Worte zu dem Programm. Ganz am Anfang wird der Grad des Interpolationspolynoms festgelegt.
Oben steht eine Routine, welche ein Lineares Gleichungssystem auflöst. Es ist das Gauss-Verfahren mit Pivotwahl. Die Matrix heißt m, die Vektoren für die Messwerte xm und ym. Diese werden mit der sog Runge-Funktion

y = 1 / (1 + x²)

befüllt. Die Werte entstamme dem Bereich für x von -5 bis 5. Danach wird das Gleichungssystem aufgebaut und gelöst. Die Lösung des Gleichungssystems sind die Koeffizienten, welche hier im Computerprogramm nicht a, b, c, usw. heißen sondern a₀, a₁, a₂ usw. Schließlich wird diese Näherungslösung im Bereich -5 und 5 augegeben. Mit dieser Liste kann z.B. mit Excel eine Grafik erzeugt werden.

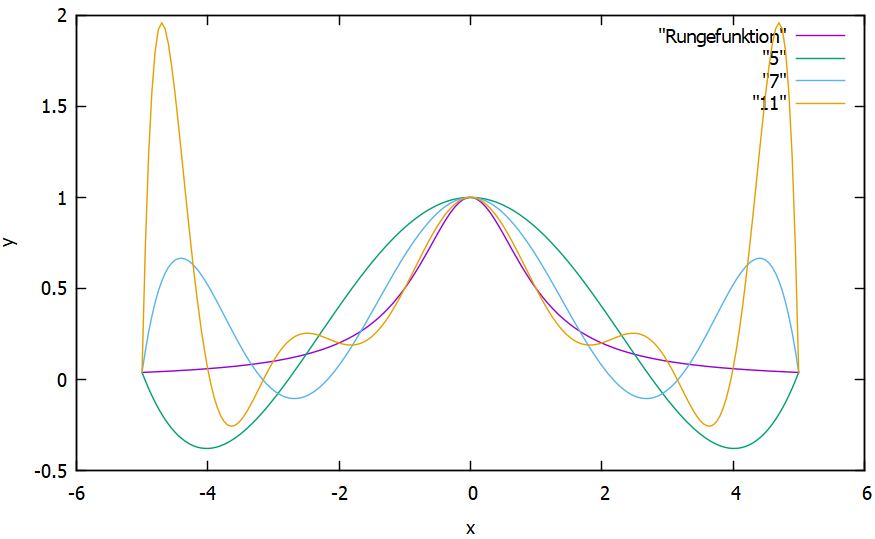
Interpolationspolynome zur Runge-Funktion. Höhere Grade neigen zum Überschwingen.

Zum Glück neigen die Polynome für astronomische Anwendungen viel seltener zum schwingen. Ich habe einmal die Rektaszension eines Kometenortes eingegeben und interpoliert. Das blieb auch bei 11. Grad glatt. Diese Eigenschaft der normalen Bahnverläufe lässt sich also ausnutzen: Für die näherungsweise Berechnung kann man Polynome hohen Grades und damit hoher Genauigkeit benutzen.

Uwe Pilz, Oktober 2019