Simulation von Bahnkurven beim Kepler-Problem

Immer wieder findet man in den Medien Meldungen über das vermeintliche Ende der Erde durch eine Asteroiden-Kollision zu einem zukünftigen Zeitpunkt xy. So meldete etwa die Tageszeitung Die Welt am 5. April 2002 eine Wahrscheinlichkeit von 1:300 eines Einschlags mit dem "Killer-Asteroiden" 1950 DA (mehr dazu) [1]. Knapp vier Monate später machte eine Kollisionsvorhersage mit dem Asteroiden 2002 NT7 für den Februar 2019 Schlagzeilen. Welcher Sternfreund kennt nicht die Fragen von Bekannten oder Kollegen nach einer möglichen Kollision? Und tatsächlich sind die Positionsbestimmung und die Bahnberechnung von Himmelskörpern die ursprünglichen Aufgaben der Astronomie. Heute werden für die Bahnbestimmung moderne Computeranlagen eingesetzt, und Rechnungen, die früher Tage dauerten, werden heute elektronisch in Sekundenbruchteilen erledigt. Um die Wichtigkeit der Wahl des "angemessenen" Rechenverfahrens bei der Lösung von astronomischen Problemen auf modernen Computern zu verdeutlichen, sollen in einer Computer-Simulation verschiedene rechnerische Verfahren zur Behandlung des Kepler-Problems aus der Himmelsmechanik qualitativ miteinander verglichen werden. Zwar gehen die heutigen Kollisionsvorhersagen nicht vom einfachen Kepler-Problem aus, sondern sie berücksichtigen die gesamte Dynamik des Planetensystems (z.B. den oft nicht zu vernachlässigenden Einfluss der großen Planeten), dennoch kann man selbst beim vereinfachten Kepler-Problem die Auswirkungen der Wahl des Rechenverfahrens leicht beobachten.

Beschreibung des Testproblems

Das Testproblem ist das bekannte Einkörperproblem aus der Himmelsmechanik. Dabei erzeugt ein massereicher Zentralkörper ein Gravitationsfeld, in dem sich ein fast masseloser Körper bewegt. Aufgrund der Massenverhältnisse wird vereinfachend angenommen, dass die Zentralmasse gänzlich unbewegt bleibt und sich nur der masseleichtere Körper bewegt, anstatt dass sich beide Körper um ihren gemeinsamen Schwerpunkt bewegen. Dieses Modell liefert brauchbare Näherungen an die wirklichen Verhältnisse in unserem Sonnensystem beim Umlauf von Planeten um die Sonne und beim Umlauf von Monden oder Satelliten um einen Planet. Zu Ehren von Johannes Kepler, der zu Beginn des 17. Jahrhunderts entscheidende Einsichten in die Bewegungen der Planeten formulierte, nennt man das Einkörperproblem auch Kepler-Problem.
Der masseleichtere Körper wird im Folgenden aus Gründen, die weiter unten ersichtlich sind, Projektil genannt. Man kann zeigen [2], dass beim Kepler-Problem als mögliche Bahnformen für das Projektil nur Kegelschnitte auftreten und zwar je nach Energie beschränkte Bahnen (Ellipsen) oder unbeschränkte Bahnen (Parabeln oder Hyperbeln).
Physikalisch wird die Bahn des Projektils durch eine Differentialgleichung (DGL) zweiter Ordnung beschrieben

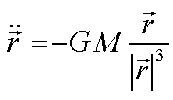
wobei der Vektor r die (zweidimensionale) Position des Projektils, G die Gravitationskonstante und M die Masse des Zentralkörpers ist.
Für das Testproblem stellen wir uns vor, dass das Projektil mit einer Anfangsgeschwindigkeit v₀ in das Zentralfeld eintritt. Die Richtung und die Größe dieser Geschwindigkeit können im Applet variiert werden. Das entspricht der Situation, dass das Projektil mit der Geschwindigkeit v₀ in das Zentralkraft eingeschossen wird und dann mit der Zentralmasse wechselwirkt.

Behandlung des Testproblems auf dem Computer

Viele numerische Verfahren behandeln lediglich Differentialgleichungen erster Ordnung, da man DGL höherer Ordnung stets zu Gleichungen erster Ordnung umformen kann. Wie das gemacht wird, findet der interessierte Leser hier. Hat man eine Differentialgleichung erster Ordnung, so kann man beispielsweise das Verfahren von Euler benutzen, um die Bahnkurve anzunähern. Dabei berechnet man nicht die ganze Bahn auf einmal, sondern nur schrittweise einige Punkte auf der Bahn - anschaulich gesprochen: man hangelt sich von Punkt zu Punkt. Neben dem vergleichweise einfachen Verfahren von Euler gibt es jedoch auch Algorithmen, die genauer arbeiten. Einige davon werden in dem Applet angeboten und lassen sich ausprobieren. Insgesamt sind in der Simulation die folgenden Verfahren anwendbar:

Verfahren von Euler
Verfahren von Heun
Runge-Kutta-Verfahren (mit/ohne kleinere Schrittweite)
Prädiktor-Korrektor-Verfahren

Je weiter unten in der Liste, desto genauer (und aufwändiger) ist das Verfahren. Das genaueste Verfahren gehört zu den sogenannten Prädiktor-Korrektor-Verfahren, die in der Praxis gerne aufgrund ihrer Genauigkeit und Effizienz verwendet werden. Der Korrektor ist übrigens benannt nach dem Mathematiker John Couch Adams benannt, der sich u.a. für astronomische Fragen interessierte und für seine genauen Berechnungen bekannt war. Wahrscheinlich hatte Adams schon ein Jahr vor Le Verrier eine Positionsbestimmung für den damals noch unbekannten Planeten Neptun, (mehr dazu).

Applet

Der Benutzer des Applets kann durch die Pull-Down-Liste das Lösungsverfahren auswählen und durch Verändern des gelben Pfeils die Anfangsgeschwindigkeit und Richtung des Projektils festlegen. Nach jeder Veränderung der Geschwindigkeit wird die exakte Bahn (dunkelgrau) des Projektils angezeigt. Durch Drücken des Start-Knopfes wird mit der Berechnung der Bahn begonnen und das Projektil bewegt sich Schritt für Schritt so wie es das numerische Verfahren bestimmt. Entgegen der Wirklichkeit bestimmt also hier die Näherungsrechnung des Computers die Bahn des Projektils. Die näherungsweise bestimmte Bahn kann mit der exakten Bahn verglichen werden und je nach Verfahren und Anfangsgeschwindigkeit erheblich abweichen.

Applet Download (setup.exe)

Beobachtungen

Nach vielen Rechenschritten werden selbst die genaueren Verfahren fehlerhaft. Die Verfahren unterscheiden sich durch die Dauer, für die sie brauchbare Näherungen liefern. Weil sich die Näherungsfehler bei jedem Verfahren Schritt für Schritt aufsummieren, sind Prognosen über sehr große Zeiträume mit numerischen Verfahren prinzipiell unmöglich. Man kann lediglich feststellen, dass je genauer das Verfahren ist, desto länger lassen sich die Bahnen vorherbestimmen. Neben dem numerischen Näherungsfehler (der menschen- und maschinengemacht ist) hat man in den vergangenen Jahren herausgefunden, dass die Planetenbahnen des Sonnensystems naturgegeben chaotisch sind und sich daher Langzeitprognosen verbieten, vgl. z.B. [3].

Besonders fatal für eine Kollisionsvorhersage ist die Situation bei der die korrekte Bahn das Projektil auf die Zentralmasse führt, während das gewählte numerische Verfahren jedoch einen Vorbeiflug voraussagt. Diese Situation ist in Abbildung 1 dargestellt. Als numerisches Verfahren wurde dort das Verfahren von Heun verwendet. Das Beispiel soll illustrieren, dass blindes Vertrauen in die Ergebnisse numerischer Rechnungen ohne eine Analyse der Fehlerträchtigkeit der verwendeten Verfahren völlig unangebracht ist.

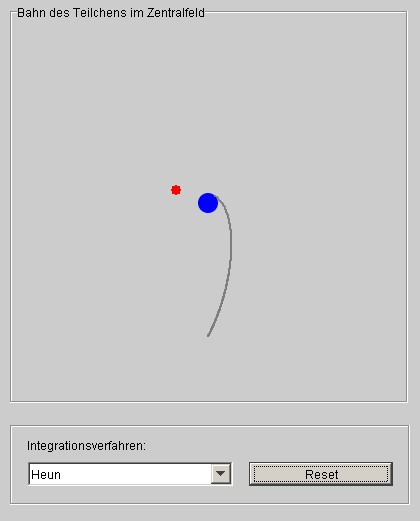
Abbildung 1: Folgenschwere Fehlvorhersage: die exakte Bahn (dunkelgrau) endet auf der Zentralmasse und das numerische Verfahren sagt einen Vorbeiflug voraus.

Danksagung

Die Simulation ist aus dem Numerix-Projekt unter der Leitung von Prof. Dr. F. Locher des Fachbereichs Mathematik der Fernuniversität Hagen hervorgegangen, bei dem ich mich für die freundliche Unterstützung bedanken möchte.

(Ralph Brinks) Vgl. VdSJ 13, S.49.

[1] Tageszeitung "Die Welt" vom 5.4.2002, "Weltuntergang am 16. März 2880?"
[2] Guthmann, Andreas: Einführung in die Himmelsmechanik und Ephemeridenrechnung, BI Verlag, Mannheim, 1994
[3] Murray, N., Holman, M: The Role of Chaotic Resonances in the Solar System, Nature, vol. 410, April 2001.