Startseite | Programm-Archiv | Algorithmus Koordinatentransformation | Unserer Vorläufer | Kontakt, Datenschutz

Das Weltall ist ein Kreis,
dessen Mittelpunkt überall,
dessen Umfang nirgends ist.
Blaise Pascal

Drehung von Koordinatensystemen

In der Astronomie ist es häufig nötig, von einem kartesischen Koordinatensystem in ein anderes zu wechseln, ohne den Koordinatenursprung zu wechseln. Der feste Ursprung kann dabei die Sonne oder die Erde sein. Ich gebe hier an einem Beispiel die Formelsätze an, umd diese Transformation auszuführen.

Eine solche Transformation wird durch die Drehung um drei Winkel vorgenommen. Diese Winkel nennt man Euler-Winkel. Die Drehung ist keineswegs eindeutig: Es gibt mehrere Wege zum Ziel und somit mehrere Sätze von Euler-Winkeln für dieselbe Transformation. In der Astronomie benutzt man als Drehachse eine der drei Koordinatenrichtungen des jeweils neuen Systems, in welchem man zwischendrin gerade angekommen ist. In der Luftfahrt, Seefahrt und Fahrzeugtechnik benutzt man hingegen stets körperfeste Koordinaten. Ich habe diese drei Winkel in den beigelegten Programmausschnitten mit α, β und γ bezeichnet. In Abhängigkeit der Transformation haben sie meist eine wirkliche Bedeutung.

Drehung mit Bahnelementen

In der Astronomie sind die Drehwinkel in den Bahnelementen verankert. Als Beispiel wähle ich die Koordinatentransformation des Planeten Mars am 31, März 2017, 0 h UT von Bahnkoordinaten (Kepler-Ellipse) in heliozentrische Koordinaten.

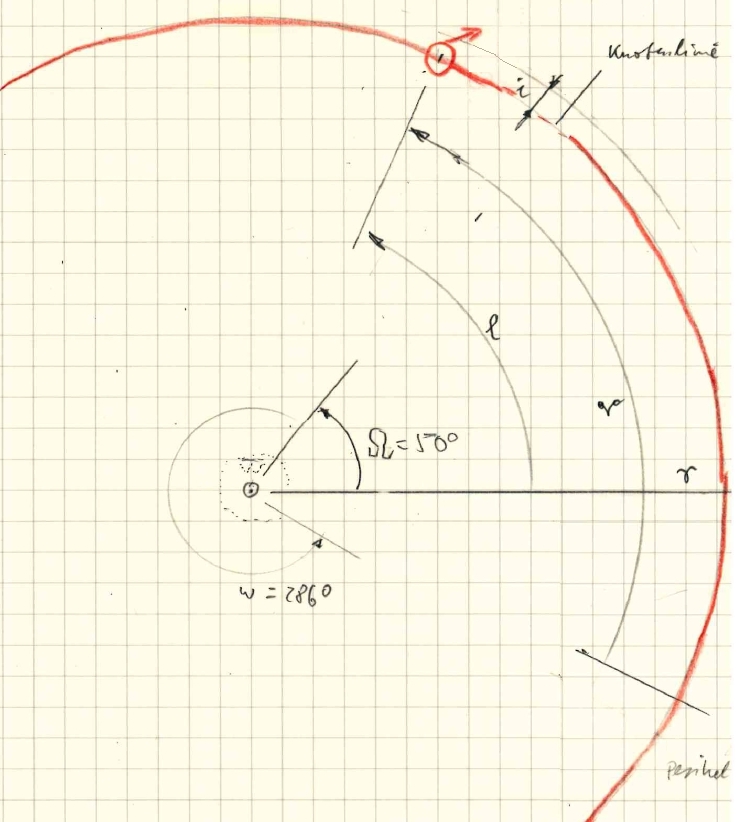
Die Lage des Mars in der Bahn wird durch die Kepler-Gleichung bestimmt. Man bekommt als Ergebnis einen Winkel, die sog. wahre Anomalie ν (der griechische Buchstabe nu). Dies ist der Winkel des Planeten, gemessen von seinem sonnennächsten Punkt, dem Perihel. Eine andere Orientierungsmöglichkeit bietet die Bahn selbst nicht. Außerdem ist noch der Sonnenabstand r bekannt. Diese Größe ändert sich während der Transformation nicht.

Um hieraus die heliozentrischen Koordinaten l und b zu gewinnen, ist die Drehung um drei Winkel nötig:

1) Drehung um das Argument des Perihels ω (entspricht α)
2) Drehung um die Bahnneigung i (entspricht β)
3 Drehung um die Länge des aufsteigenden Knotens Ω (entspricht γ)

Die wahre Anomalie des Mars betrug am angegebenen Datum ν=91,22°, der Sonnenabstand r=1,512 AE. Hieraus müssen zunächst kartische Koordinaten bestimmt werden:

x0 = r cos ν = -0,032 AE
y0 = r sin ν =  1,511 AE
z0 =0

Die Drehungen erfordern die Sinus- und Kosinuswerte der Drehwinkel. Damit die Formeln in den Python-Programmen nicht so unübersichtlich werden, habe ich diese Werte auf Variablen gelegt. Dabei ist sA der Sinus von α und cG der Kosinus von  γ, die anderen Werte entsprechend.

Programmschnipsel für die erste Drehung um ω:

x1 = cA * x0 - sA * y0
y1 = sA * x0 + cA * y0
z1 = z0

Als Drehwinkel wird das sog. Argument ind nicht die Länge des Perihels benutzt. Dieses ist der Winkel zwischen Perihel und aufsteigendem Knoten. Da dies die erste notwendige Drehung ist, wird dieser Wert oft in den Bahnelementen angegeben, anstelle der eigentlich "logischeren" Knotenlänge.

Nach dieser Drehung zeigt die neue x-Achse in Richtung des Perihels. Die Zwischenwerte sind:

x1=1,44 AE
y1=0,4533 AE
z1=0

Der Winkel zwischen der Knotenlinie und dem Mars beträgt ca. 17°, das kann man in der Grafik nachmessen.

Die zweite Drehung erfolgt um die jetzt neue x-Achse um die Bahnneigung i:

x2 = x1
y2 = cB * y1 - sB * z1
z2 = sB * y1 + cB * z1

Danach liegen die Koordinaten bereits in der Ekliptik-Ebene, zeigen aber noch nicht auf den Frühlingspunkt:

x2=1,44 AE
y2=0,4531 AE
z2=0,015 AE

Die letzte Drehung erfolgt um die z-Achse z2, um das Koordinatensystem zum Frühlingspunkt zu orientieren. Der Drehwinkel ist die Länge des aufsteigenden Knotens Ω, im Programm γ:

x3 = cG * x2 - sG * y2
y3 = sG * x2 + cG * y2
z3 = z2

Das Ergebnis ist

x3=0,591 AE
y3=1,391 AE
z3=0,015 AE

Aus diesen lassen sich die heliozentrischen Winkel ausrechnen:

b=asin(z/r) = 0,55°
l=atan(y3/x3)=67,0°

Statt des Arkustangens sollte in Programmiersprachen die atan2-Funkion benutzt werden, welche die Quadranten richtig berücksichtigt. Auf besseren Taschenrechnern gibt es eine Rechteck-Polar-Umwandlung, die dasselbe leistet. Bei meinen Casio-Taschenrechnern heißt sie Pol(x,y).

Die drei obigen Formeln kann man auch in eine Gesamtformel packen:

x3 = x0 * (cG * cA - sG * cB * sA) + y0 * (-cG * sA - sG * cB * cA) + z0 * (+sG * sB)
y3 = x0 * (sG * cA + cG * cB * sA) + y0 * (-sG * sA + cG * cB * cA) + z0 * (-cG * sB)
z3 = x0 * sB * sA + y0 * sB * cA + z0 * cB

Mitunter ist es nötig, den umgekehrten Weg zu gehen und eine Rücktransformation auszuführen. Die Gesamtformel hierfür ist:

x0 = x3 * (+cG * cA - sG * cB * sA) + y3 * (+sG * cA + cG * cB * sA) + z3 * (sB * sA)
y0 = x3 * (-cG * sA - sG * cB * cA) + y3 * (-sG * sA + cG * cB * cA) + z3 * (sB * cA)
z0 = x3 * sG * sB - y3 * cG * sB + z3 * cB

Drehung aus Sicht der Flugsteuerung

Aus der Luftfahrt wurden die Bezeichnungen für körperfeste Winkel in die Seefahrt und die Fahrzeugtechnik übernommen. Man spricht von Roll- Nick- und Gierwinkel:

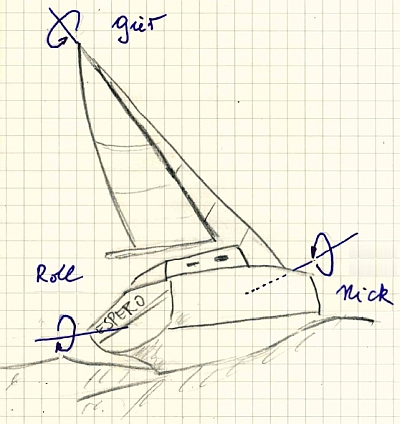
Eine Drehung kann man zum Beispiel so vornehmen, dass zuerst der Gierwinkel korrigiert wird. Damit stimmt schon mal die Richtung zum Ziel, der sog. Steuerkurs. Als nächstes wird um den Nickwinkel gedreht, damit ist die Längsachse z.B. waagerecht und nicht mehr gen Meeresboden gerichtet. Damit der Kaffee nicht aus den Tassen schwappt, korrigiert man zuletzt den Rollwinkel.

Man kann aber auch in einer anderen Reihenfolge vorgehen.

Die Formeln für die Hintransformation sind:

x1 = cA * x0 - sA * y0 
y1 = sA * x0 + cA * y0 
z1 = z0

x2 = cB * x1 + sB * z1
y2 = y1
z2 = -sB * x1 + cB * z1

x3 = x2
y3 = cG * y2 - sG * z2
z3 = sG * y2 + cG * z2

Und wieder für die Rücktransformation:

x1 = x3
y1 =  cG * y3 + sG * z3
z1 = -sG * y3 + cG * z3


x2 = cB * x1 - sB * z1
y2 = y1
z2 = sB * x1 + cB * z1

x3 =  cA * x2 + sA * y2
y3 = -sA * x2 + cA * y2 
z3 = z2

Uwe Pilz, März 2021