Alles was lediglich wahrscheinlich ist,
ist wahrscheinlich falsch.
René Descartes

Ausgleich mit Polynomfunktionen

Für die Annäherung vom Messerwerten oder andern, nur als Tabelle vorliegenden Zahlenreihen, wird oft eine lineare Regression angenommen. Diese legt eine Gerade durch die Daten. Die Rechenumgebung hierzu ist in besseren Taschenrechenrn enthalten. Durch eine Koordinatentransformation können einige weitere Funktionen erschlossen werden, welche graphsch z.B. im Übergang zu halb- oder doppeltlogarithmischen Millimeterpapier entstehen

Polynome sind Funktionen der Art

y = c₀ + c₁ x + c₂ x² + c₃ x³ ...

Damit lassen sich Kurvenverläufe annähern, welche sich mit den linearisierbaren Funktionen schwer abdecken lassen. Wir sollten aber beachten, dass höhere Polynome selten den physikalischen Gegebenheiten entsprechen. Es ist meist keine gute Idee, eine physikalisch abwegige Funktion zur Glättung von Tabellenwerte zu benutzen. Eine quadratische Funktion kann man jedoch meist nehmen, sie deckt neben dem Anstieg auch noch die Wölbung ab. Auch mit einer Funktion dritten Grades erlebt man nur selten Schiffbruch. Funktionen höheren Grades (also größer als 4) neigen zu seltsamen Effekten. Die Messpunkte selbst werden zwar ganz gut getroffen, aber dazwischen entwickelt die Funktion ein Eigenleben: Sie neigt zum Schwingen.

Ein erstes Zeichen für diese Art von Instabilität zeigt sich, wenn man die Einganswerte / Messwerte leicht rundet. Falls dann ganz andere Koeffizienten entstehen, dann ist das bei der Berechnung entstehende Gleichungssystem "schlecht konditioniert". Es ist, als wolle man auf dem Kästchenpapaier den Schnittpunkt zweier Geraden ermitteln, die sichunter einem sehr spitzen Winkel schneiden.

Ich habe im Programmarchiv ein Python-Programm hinterlegt, welches den Polynomausgleich ausführt. Die Matehmatik hierzu wird ganz gut in einem Aufsatz von Gerhard Krucker dargesetllt (ab. Seite 10).

Alle Eingangswerte müssen direkt im Programmcode hinterlegt werden:

######## Eingaben hier ################################################

n = 3 # Grad des Polynoms
m = 6 # Anzahl Datenpunkte

# die Messwerte
x = [5.2, 4.2, 3.2, 2.3, 1.46, 0.48]     
y = [2.41, 2.87, 3.55, 4.50, 6.14, 9.35]

initKoor(0,6,1, 0,12,1) # initKoor(xMin,xMax,xScala, yMin,yMax,yScala)

########################################################################

Die hier hinterlegten Messwerte stellen übrigens die atmosphäreische Refraktion der Winteratmosphäre in einer Höhe von ca. 200 Meter ü. NN dar.

Wenn man für das Koordinatensystem vernünftige Werte einsetzt, dann wird das Ergebnis für die gegebenen x-Werte angezeigt. Damit kann man schauen, ob man "seltsame Effekte" hat:

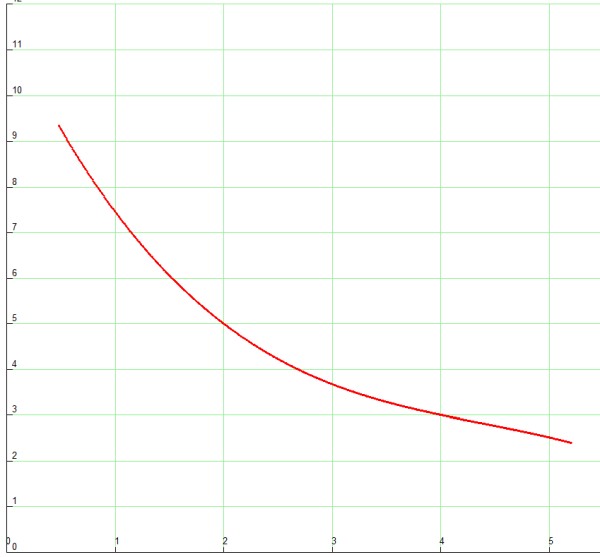
Obwohl das Beispiel nur dritten Grades ist, sieht man bei x=5 die leichte Tendenz der Kurve, nach unten abzuweichen.

Uwe Pilz, November 2020