Taylor-Reihen

Mit Taylor-Reihen kann man alles berechnen!

... nun gut, fast alles.

Eine Taylor-Reihe ist eine Polynomfunktion, also eine Reihe, in der alle Potenzen von x mit einem Koeffizienten versehen sind:

y = a₀ + a₁·x + a₂·x² + a₃·x³ + ...

Es gibt eine große Klasse von Funktionen, die man durch diese Reihe mit beliebiger Genauigkeit nachbilden kann, wenn man genügend viele Glieder der Reihe berücksichtigt. Solche Funktionen nennt man analytische. Hierunter finden sich das meiste, mit dem man in Wissenschaft und Technik zu tun hat.
Die Idee dahinter: Wenn die Reihe und die Funktion an der Stelle x=0 im Funktionswert und in allen Ableitungen übereinstimmen, dann nähern sie sich immer stärker an. Bei Berücksichtigung von unendliche vielen Gliedern werden die meisten Funktionen wirklich identisch.
Dazu müssen aber alle (also unendlich viele) Glieder der Reihe berücksichtigt werden. Für praktische Anwendungen kommt man aber mit endlich vielen Gliedern schon sehr weit. Die Standardfunktionen wie die Exponentialfunktion oder die Winkelfunktion werden in Computerprogrammen oder sogar im Taschenrechner meist mit Taylor-Reihen berechnet. Dazu muss man nur die passenden Koeffizienten a₁, a₂, usw. kennen.

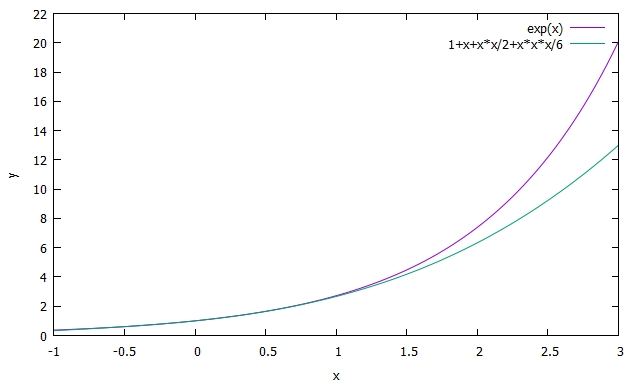
Wie bestimmt man die Koeffizienten?

Die Exponentialfunktion und eineTaylorentwicklung mit vier Gliedern

Die Koeffizientenformel ergibt sich aus der Forderung, dass die Ableitungen der anzunähernden Funktion und des Polynoms an der Stelle x=0 gleich sein sollen. Dazu muss man die Ableitungen der anzunähernden Funktion f(x) berechnen. Hierbei hilft der Ableitungsrechner [1]. Die ersten Koeffizienten sind
        a₀ = f(0),              also der Funktionswert an dieser Stelle
        a₁ = f '(0),             also der Anstieg
        a₂ = f ''(0) / 2,     das ist die Hälfte der Krümmung
        a₃ = f '''(0) / 6

Allgemein gilt
        a_n = f⁽ⁿ⁾(0) / n!

Hier ist f ⁽ⁿ⁾ die n-te Ableitung der abzubildenden Funktion und n! die Fakultät von n, also das Produkt aller Zaheln von 1 bis n.

Ein Beispiel

Besonders einfach lässt sich die Taylor-Reihe der Exponentialfunktion f(x) = e^x berechnen. Diese Funktion hat die Eigenschaft, dass ihre Ableitung wieder e^x ist, und alle weiteren Ableitungen auch. Diese Ableitung benötigen wir nur an einer Stelle, nämlich x=0, also e⁰, was den Wert 1 ergibt. Alle Ableitungen haben also den Wert 1.

Die Exponentialfunktalfunktion lässt sich also annähern durch
e^x = 1/0! + x/1! + x²/2! + x³/3! + ...

Hier habe ich für den Funktionswert selbst (die "nullte Ableitung") den Wert 0! ergänzt. Es gilt 0!=1, so dass alles richtig bleibt und die Formel für alle Glieder gleich ist.

Für diese einfache Formel lege ich ein kleines Python-Programm hierher. Damit könnt ihr ausprobieren, wieviele Glieder der Taylor-Reihe ihr benötigt, um e^x mit einer vernünftigen Genauigkeit zu bestimmen. Wie nicht anders zu erwarten war: Je weiter man sich von x=0 entfernt, desto mehr Gleider werden gebraucht. Das wird irgendwann unpraktisch, so das man weitere mathematische Tricks suchen muss, um die Taylorentwicklung auf einen kleinen Bereich um x=0 zu beschränken. Mit Hilfe der Potentgesetze ist das kein Problem, so dass der Taschenrechner auch e¹⁰⁰ zügig berechnet.

# Exponentialfunktion mit Taylor-Entwicklung
from math import *
while (1==1):
    x=float(input("x-Wert:"))
    n=int(input("Anzahl Glieder:"))
    fak=1 
    sum=1 
    potenz=1
    for i in range (1,n):
        fak=fak*i
        potenz=potenz*x
        sum=sum+potenz/fak
    print("Näherung", sum, "exakt", exp(x))

In diesem Programm berechne ich sowohl die Fakultät als auch die Potenz nicht für jedes Glied von Grund auf neu (wie es die Formel angibt), sonern führe sie schrittweise mit. Das spart Rechnezeit. Damit man ein wenig experimentieren kann, bleibt das Programm ewig in der Rechnschleife und muss mit strg-c abgebrochen werden.
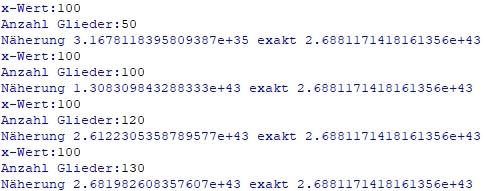
Man kann damit auch ausprobieren, wieviele Glieder man für e¹⁰⁰ benötigt. es sind über 120:

Annäherung bis in alle Unendlichkeit?

Kann man von der sogenannten Entwicklungsstelle x=0 nun alle Werte der gewünschten Fnktion besteimmen, von praktischen Schwierigkeiten einmal abgesehen?
Für einige Funktionen geht das tatsächlich, die Exponentialfunktion ist ein Beispiel, für die Winkelfunktionen Sinus und Kosinus gilt das auch. Es gibt aber auch andere Beispiele, ich habe y=1/x ausgewählt. Diese kann um den Wert 0 herum nicht entwickelt werden, da sie dort nicht definiert ist. Man behilft sich in solchen Fällen damit, dass man einfach den Entwicklungspunkt verschiebt, und stattdessen die Taylorentwicklung für y=1/z angibt, wobei z.B. z=1-x. Die Reihe wird also um den Punkt x=-1 entwickelt und lautet:
1/z = 1/(1-x) =1+ z + z² + z³ + z⁴ + z⁵ ...

Für z=-1 nähert sie sich sie sich x=0, also der Unstetigkeitsstelle. Es ist intuitiv verständlich, dass es die Funktion nicht schafft, die Unstetigkeitsstelle bei z=1 (also x=0) zu überwinden und von plus Unendlich nach minus unendlich zu springen: Eine SIngularität begrenzt das Konvergenzintervall immer. Interessanterweise "schafft" es die Reihe aber auch nicht, über die ganz harmlose Stelle bei x=2 zu kommen! Dies liegt daran, dass eine Taylorreihe – wenn überhaupt – nur in einem Intervall konvergiert, welches symmetrisch zur Entwicklungsstelle ist.

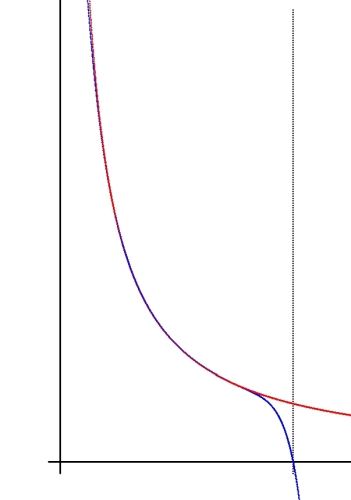
Die Funktion 1/x (rot) und die ersten 10 Glieder ihrer Taylor-Entwicklung (blau). Die Taylor-Reihe funktioniert nur zwischen 0 und 2(gestrichelte Hilfslinie)

Das muss man alles mal erlebt haben, deshalb gibt es auch hierzu wieder ein kleines Python-Programm:

# Exponentialfunktion mit Taylor-Entwicklung
# 1/x mit Taylor-Entwicklung
from turtle import *
from math import *

def plot(x,y, pc): # einen Punkt setzen
    pencolor(pc)
    penup()
    goto(200*x-350,200*y-350)
    pendown()
    dot(2) 
def plotBlue(x,y):  # in Blau
    plot(x,y,"blue")
def plotRed(x,y):   # in Rot
    plot(x,y,"red")
def plotBlack(x,y): # in Schwarz
    plot(x,y,"black")

tracer(0,0) # Bildschirmaktualisierung aus

# ein kleines Koordinatensystem
y=-0.1	# y-Achse
for j in range (5100):
    plotBlack(0,y)
    y=y+0.001
y=-0.1 	# Hilfslinie bei y=2
for j in range (200):
    plotBlack(2,y)
    y=y+0.02
x=-0.1	# x-Achse
for j in range (5100):
    plotBlack(x,0)
    x=x+0.001

# die eigentliche Rechnung    
n=5 # Anzahl der Taylor-Koeffizienten, hier ändern
x=0.001
for j in range (5000):
    x=1-x
    sum=1 
    potenz=1
    for i in range (1,n):
        potenz=potenz*x
        sum=sum+potenz
    x=1-x
    x=x+0.001
    plotBlue (x, sum) 	# Näherung: blau
    plotRed(x,1/(x))	# Exakt: rot

update() # Bildschirm anzeigen

Ihr seht: Das Polynom funktioniert nur zwischen 0 und 2. Man kann dieses Verhalten zwar ausrechnen, aber ich erspare uns das hier. Aber die Botschaft lautet: Taylor-entwicklungen funktionieren am besten (oder überhaupt nur) in der Umgebung der Stellen, an der man sie – ggf. nach einer Koordiantenverschiebung – entwickelt.

(Uwe Pilz, Dezember 2018)

Literatur

[1] www.ableitungsrechner.net