A&A Title Image Startseite | Programm-Archiv | Algorithmus Trojanert | Unsere Vorläufer | Kontakt, Datenschutz

Jupiters Exzentrizität und die Trojaner

erschienen im VdS-Journal 16, verfasst von Helmut Jahns

 Die meisten Asteroiden umlaufen die Sonne im sogenannten Hauptgürtel zwischen den Bahnen des Mars und Jupiter. Auf einige trifft dies jedoch nicht zu: es gibt eine Gruppe von Asteroiden mit ähnlichen Sonnenabständen und somit ähnlichen Umlaufzeiten wie Jupiter. Sie werden als Trojaner-Asteroiden, oder auch kurz als Trojaner (ihre Namen rühren von Helden aus der Erzählung von der Schlacht um Troja her).

Normalerweise werden die Bahnen solcher Himmelskörper durch die Schwerkraft Jupiters in kurzer Zeit so sehr gestört, daß sich ihr mittlerer Sonnenabstand stark ändert oder die Asteroiden gar auf Kollisionskurs mit anderen Himmelskörpern gebracht werden. Die Trojaner hingegen können sich dieser fatalen Schwerkraftwirkung dieses massereichsten Planeten im Sonnensystem entziehen. Daß dem so ist, verdanken sie einer himmelsmechanischen Besonderheit: der französische Mathematiker und Astronom Joseph-Louis Lagrange (1736 bis 1813) entdeckte Ende des 18. Jahrhunderts, daß es in einem System zweier sich umlaufender Körper wie Sonne und Planet insgesamt fünf Punkte gibt, in denen sich die beteiligten Gravitationskräfte und die Fliehkraft genau aufheben. Ein dritter masseloser Körper sollte demnach in diesen Punkten verharren können. Diese fünf Punkte werden gemeinhin als die Lagrange- oder auch Librationspunkte bezeichnet und mit L1 bis L5 durchnumeriert. Die Anordnung dieser Punkte ist in Abb. 1 skizziert, wobei die Perspektive synchron zu Jupiters Sonnenumlauf mitrotiert, d.h. die Verbindungslinie zwischen Sonne und Jupiter ruht in dieser Grafik.


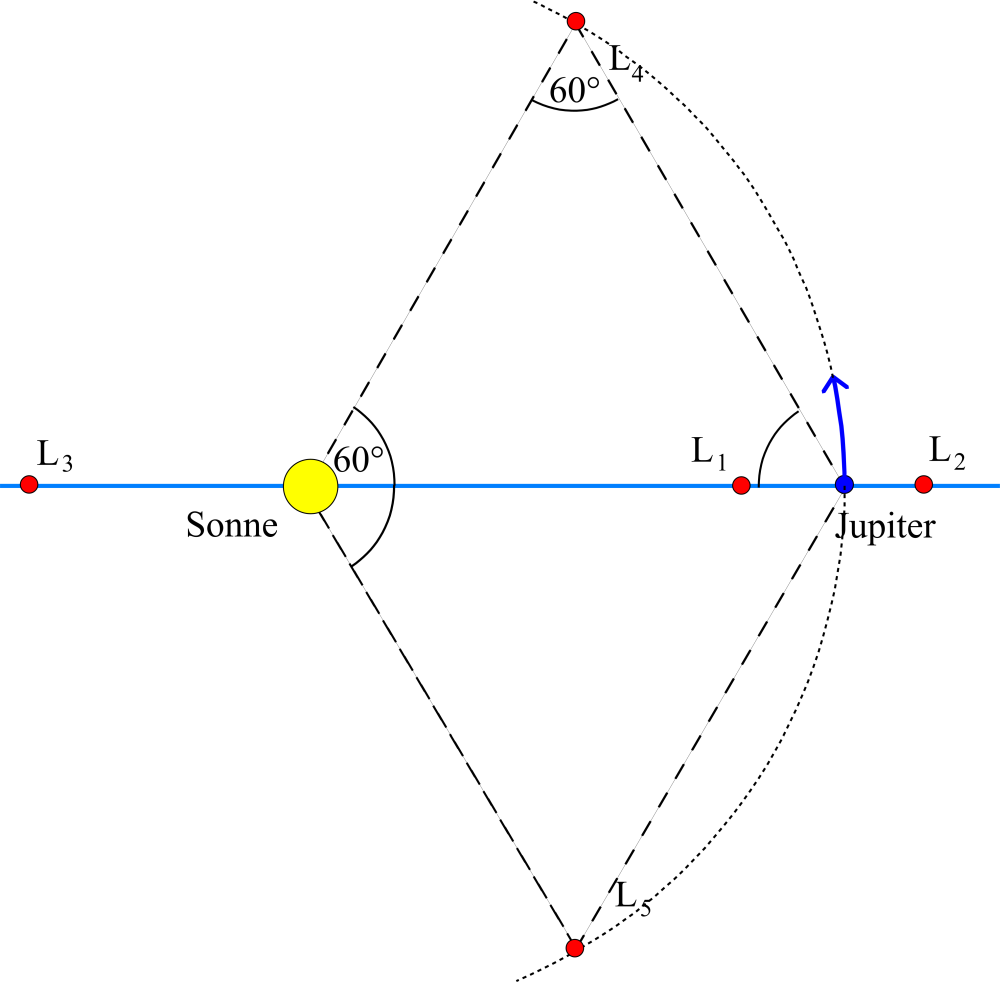
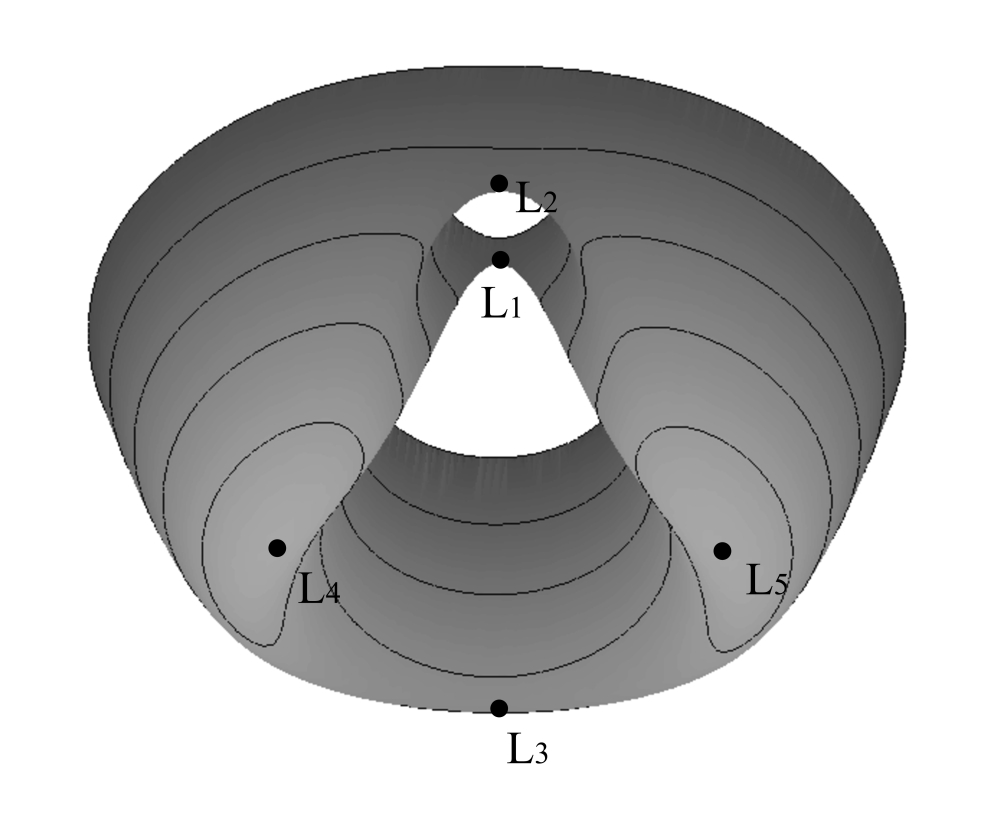
Abb.1 Die Lage der Lagrange-Punkte. Die Punkte L1 bis L3 befinden sich auf der Verbindungslinie Sonne-Jupiter, während die Punkte L4 und L5 jeweils ein gleichseitiges Dreieck mit der Sonne und Jupiter aufspannen. Das Bezugssystem dieser Darstellung rotiert synchron zu Jupiters Umlauf um die Sonne, so daß die blau gezeichnete Verbindungslinie Sonne-Jupiter in diesem Bezugssystem sich in Ruhe befindet.

Bei den Lagrange-Punkten L2 und L3, die sich exakt auf der Verbindungslinie befinden, liegen die Dinge recht klar: die Fliehkraft und die Summe der Schwerkräfte wirken darin genau entgegengesetzt und sind vom Betrag her genau gleich. In L1 heben sich hingegen die Schwerkräfte gegenseitig auf, während keinerlei Fliehkraft wirkt. Weniger anschaulich sind die Verhältnisse bei L4 und L5: hier wirkt die Schwerkraft in Richtung der Verbindungslinie, während die Fliehkraft entgegengesetzt wirkt. In L4 und L5 sind diese Kräfte genau gleich stark und heben sich ebenfalls zu null auf.


Abb.2 Graviationspotential des Trojanerproblems. Eingezeichnet sind außerdem die stabilen Lagrange-Punkte L4 und L5, sowie die instabilen Punkte L1 bis L3.

In Abb.2 ist das effektive Potential inkl. der Lagrange-Punkte in einer Ansicht von unten dargestellt. Es ist kein reines Gravitationspotential, da die Fliehkraft ebenfalls Berücksichtigung findet. Die Kraft auf einen dritten Körper wirkt bei solchen Potentialen stets in Richtung des größten Gefälles, ähnlich wie eine Kugel, die in einem entsprechend geformten Relief frei rollen kann. Demnach sind die Lagrange-Punkte L1 bis L3 (die Sattelpunkte im Potential) instabil. Für einen dort plazierten Körper genügt der kleinste Stoß, um ihn zunächst langsam, dann immer schneller von dort hinweg bewegen zu lassen. Im Gegensatz dazu besitzt das Potential bei L4 und L5 Mulden, weshalb ein sich dort befindlicher dritter Körper auch bei kleineren Auslenkungen in der Nähe dieser Punkte verbleibt. Die Trojaner befinden sich ausnahmslos in den Einzugsbereichen der Lagrange-Punkte L4 und L5.

Die Bahn des Jupiter ist nicht kreisförmig, sondern leicht elliptisch. Bei den bisherigen Betrachtungen wurde der Anschaulichkeit halber darauf nicht weiter eingegangen. Als Maß für die Abflachung einer Ellipse gegenüber einem Kreis gilt die Exzentrizität e. Die Werte für e bei Ellipsen liegen zwischen 0 und 1, wobei der Wert 0 einem Kreis entspricht und Werte nahe bei 1 auf sehr langgezogenen Ellipsen hinweisen. Jupiters Exzentrizität eJup beträgt etwa 0,049. Trojaner können also auch bei nicht-kreisförmigen Bahnen eines Planeten existieren. Gilt dies auch für größere Werte für die Exzentrizität eJup einer nunmehr hypothetischen Jupiterbahn? Es fällt schwer, sich vorzustellen, daß Trojaner bei beliebig langgezogenen Ellipsen existieren. Dies wurde nun mit einer Computersimulation und einem statistischen Auswerteverfahren untersucht.

Die Simulation

Trojaner haben die Eigenschaft, daß die Große Halbachse a ihrer Bahnellipsen, also ihr mittlerer Sonnenabstand, ähnlich ist zu der des Jupiter (s. Abb. 3). Wenn man nun eine bestimmte Anzahl an Testkörpern auf ein Intervall von a verteilt, welches die Große Halbachse des Jupiter umschließt, so werden diejenigen Testkörper, die sich nicht um die Lagrange-Punkte L4 und L5 bewegen, nahe Begegnungen mit Jupiter erfahren und durch seine Schwerkraft aus diesem Bereich entfernt. Im Laufe der Zeit bleiben im wesentlichen die gebundenen Bahnen, also die Trojaner, übrig. Die Anzahl der verbleibenden Trojaner wird als Maß für die Größe des Einzugsgebietes von L4 und L5 angesehen.

Abb.3 Oben: In der Literatur ist oft zu lesen, daß Trojaner ihren Librationspunkt auf bananenförmigen Bahnen umlaufen. Tatsächlich sind es eher verschlungene Bahnformen, wobei lediglich die Einhüllende der Bahn eine Bananenform aufweist. Geplottet wurde die Bahn des Trojaner-Asteroiden (624) Hektor über 100 Jahre. Unten: Momentaufnahme der Positionen von Trojanern um L5. Trojaner können relativ große Abstände zu den Lagrange-Punkten einnehmen.

Ausgangspunkt ist das in [3] beschriebene Programm zur Numerischen Integration. Es erlaubt die Integration großer Teilchenscharen und mußte für Auswertungszwecke nur geringfügig abgeändert werden. Es wurden insgesamt 72 000 als masselos angenommene Testkörper mitintegriert. Die Testkörper wurden in einem Intervall von 5.1 bis 5.4 für die Große Halbachse a, 0 bis 0.8 für die Exzentrizität eJup und 0° bis 360° für die Mittlere Anomalie M (M ist ein Winkel und gibt im wesentlichen die Position eines Objekts auf seiner Ellipse an) verteilt. Es wurden mehrere Rechengänge durchgeführt, wobei die Exzentrizität Jupiters bei jedem Durchlauf modifiziert wurde. Die Berechnung (Runge-Kutta-Verfahren) umfaßte bei jedem Durchgang knapp 5000 Jahre und benötigte auf dem PC ca. 18 Stunden.

Abb.4 Die Exzentrizität als Maß für die Abflachung einer Ellipse. Gegenübergestellt sind zwei Ellipsen der Exzentrizität e = 0,4 und e = 0,8. Die Große Halbachse a einer Ellipse ist definiert als die Hälfte ihrer größten Ausdehnung. S Bezeichnet die Sonne, die sich in einem der Brennpunkte der Ellipse befindet.

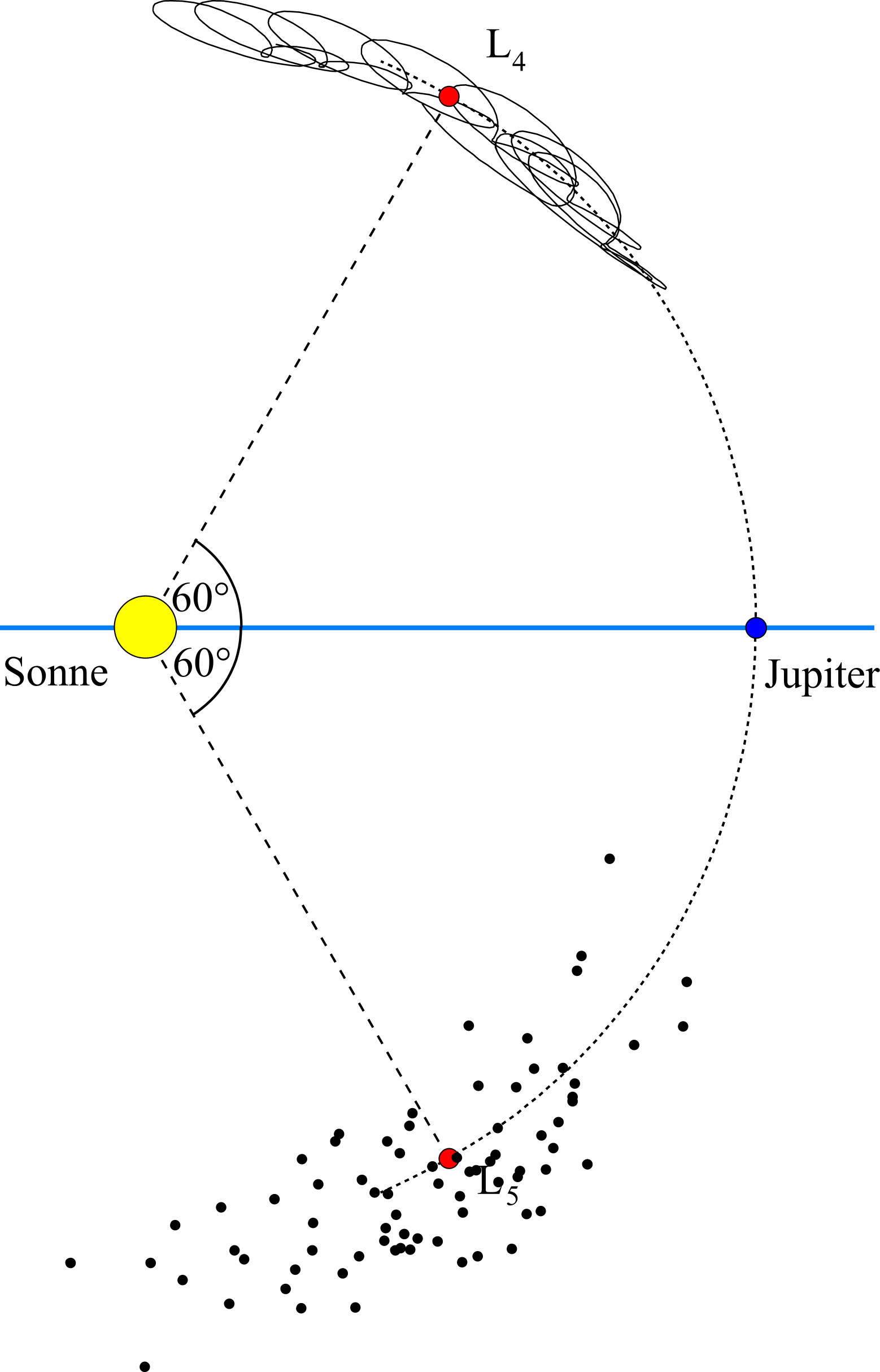
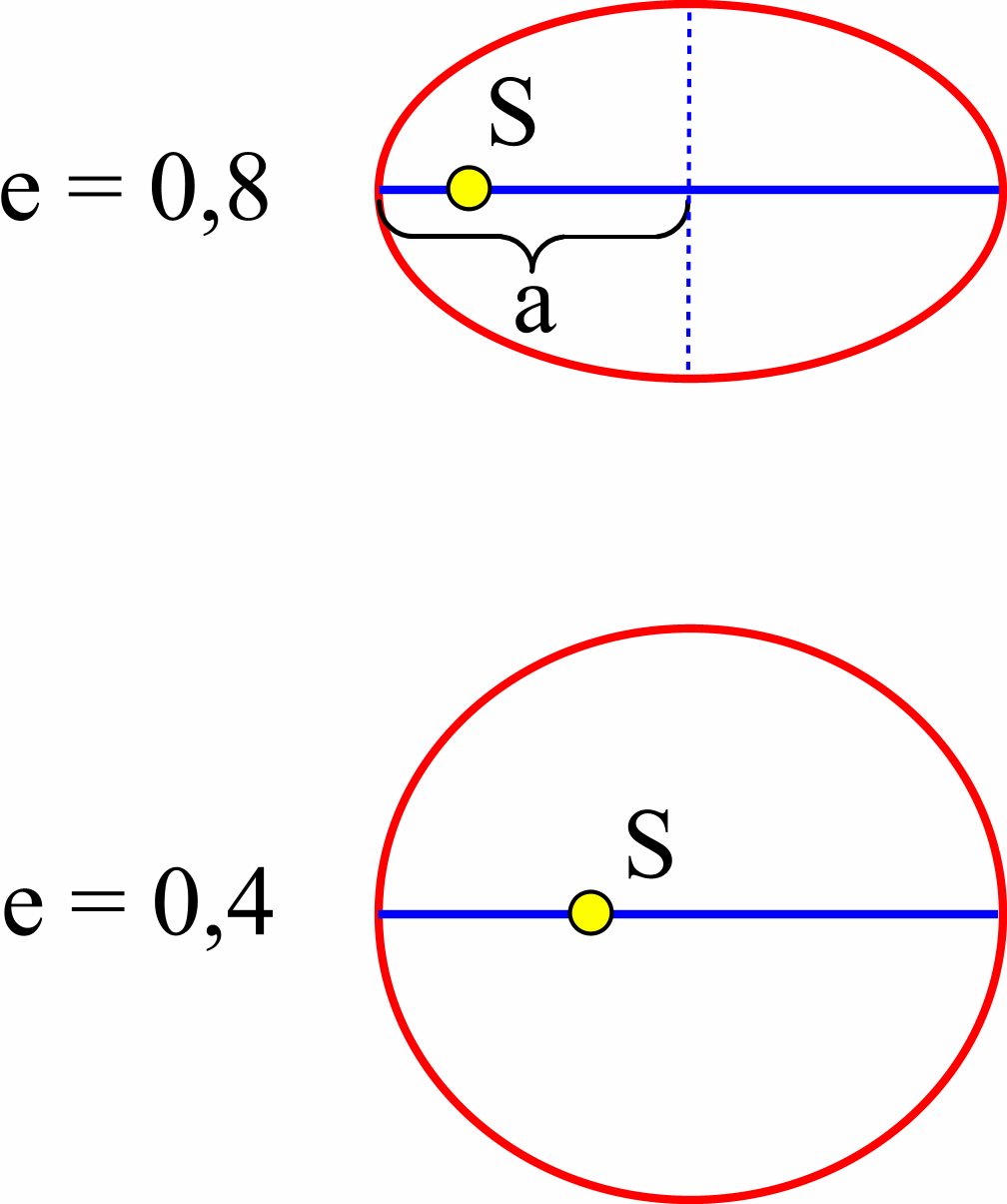
Ob ein Testkörper als Trojaner anzusehen ist, wurde anhand seiner Großen Halbachse a bestimmt; als Zugehörigkeitskriterium wurde eine maximale Abweichung 4 % von der Großen Halbachse des Jupiter genommen. Dieses Kriterium stellt sicherlich eine Vereinfachung dar und begründet sich damit, daß Nicht-Trojaner mit vergleichbaren Halbachsen wegen der Bahnstörungen nur kurze Verweilzeiten in diesem Bereich haben und somit eher seltene Erscheinungen sind.

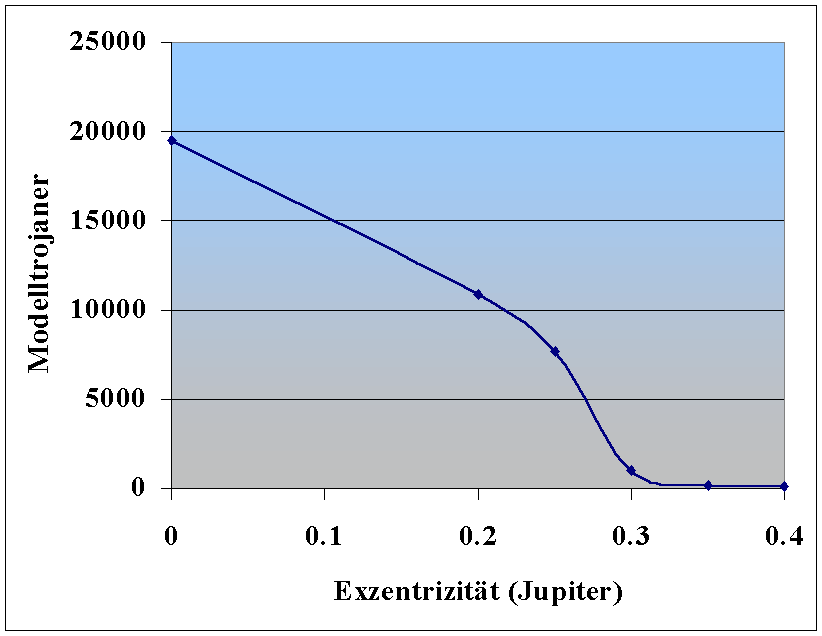
In Abb. 5 ist als Ergebnis die Anzahl der verbleibenden Modelltrojaner über eJup aufgetragen. Die Abnahme der verbleibenden Trojaner mit zunehmender Jupiterexzentrizität ist deutlich zu erkennen. Ab einer Exzentrizität von etwa 0.25 bricht die Kurve regelrecht ab. Möglicherweise befindet sich dort eine Schwelle, oberhalb der keine stabilen Trojanerbahnen mehr möglich sind. Um dies mit größerer Sicherheit aussagen zu können, muß die Rechnung mit einem optimierten Integrationsalgorithmus erneut durchgeführt werden.


Abb.5 Die Abnahme der Population von Trojanern mit zunehmender Exzentrizität des Jupiter.

Massenabhängigkeit

Man kann zeigen [1], daß Trojanerbahnen nur möglich sind, wenn die Masse des zweiten Körpers nicht mehr als etwa 3,85 % der Masse des Zentralgestirns beträgt. Beim System Sonne-Jupiter ist dies mit Sicherheit gegeben: Jupiter besitzt etwas weniger als ein tausendstel der Sonnenmasse. Beim System Erde-Mond sind die Verhältnisse nicht mehr ganz so eindeutig: der Mond besitzt rund 1,2 % der Masse der Erde, was aber von der Theorie her immer noch ausreichend ist (tatsächlich wurden in den Lagrange-Punkten des Systems Erde-Mond keine größeren Objekte, aber dafür extrem lichtschwache Wolken aus Staubpartikeln, die sogenannten Kordylewskischen Staubmonde beobachtet [2]).

Neben der Begrenzung der Planetenmassen auf kleinere Werte als 0,0385 Sonnenmassen gibt es zwei isolierte Werte für die Planetenmasse bei ca. 0,02429 und 0,01352 Sonnenmassen, bei denen ebenfalls laut analytischer Rechnung keine Trojaner geben sollte (das System Erde-Mond kommt dem zweiten Wert recht nahe). Es ist naheliegend, die Simulation zu nehmen, um diesen Sachverhalt zu überprüfen.

Die Population der Teilchenschar betrug nunmehr 9000, die über das gleiche Bahnelementintervall verteilt wurden. Die Jupitermasse mJup wurde im Bereich von 0,001 Sonnenmassen (dies entspricht in etwa dem realen Wert) bis zu 0,05 Sonnenmassen variiert.

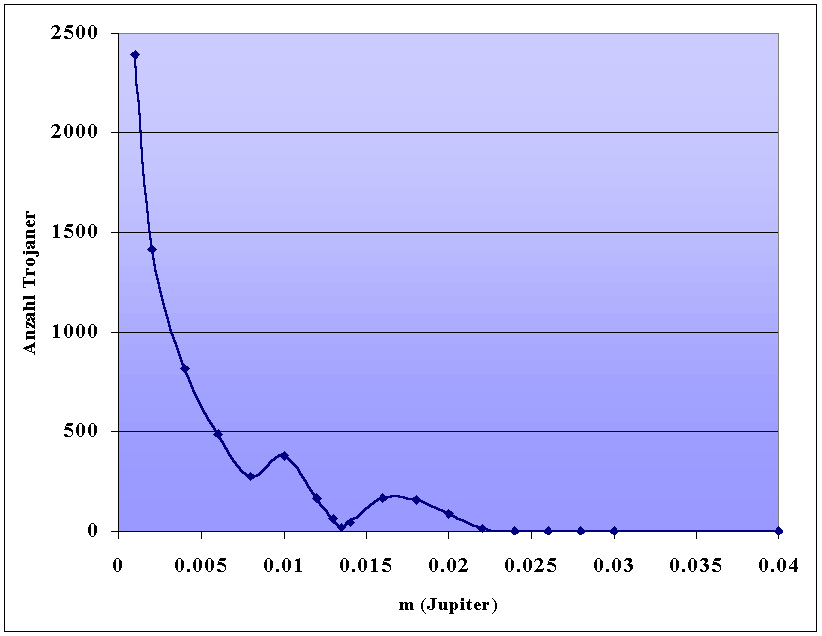
Das Ergebnis zeigt Abb. 6: neben der erwarteten Abnahme der Trojanerpopulation mit zunehmender Jupitermasse gibt es zumindest bei m2 = 0,01352 Sonnenmassen ein deutliches Minimum, während bei mJup = 0,02429 mit dieser Simulation leider keine Aussagen darüber getroffen werden kann. Bemerkenswert ist, daß die Population schon ab etwa 0,025 Sonnenmassen bereits nahezu vollständig entvölkert ist. Offenbar ist die Größe des Stabilitätsbereichs zwischen 0,025 und 0,0385 schon sehr gering.


Abb.6 Die Trojanerpopulation in Abhängigkeit von der Jupitermasse. Mit zunehmender Masse nimmt die Anzahl der Trojaner ab. Bei mJup = 0,01352 Sonnenmassen gibt es eine deutliche Einkerbung der Kurve.

Ausblick

Für die Zukunft ist angedacht, das Herzstück des Programms, den Numerikkern, um einen oder mehrere genauere und zugleich nicht wesentlich langsamere Integrationsverfahren (z.B. dem Prädiktor-Korrektor-Verfahren) zu erweitern. Obwohl man bislang auf das weniger genaue Runge-Kutta-Verfahren ausweichen muß (das ebenfalls im Programm enthaltene Bulirsch-Stoer-Verfahren ist zwar genauer, aber für derart umfangreiche Durchmusterungen zu langsam), kann man mit der vorhandenen Engine schon sehr interessante Phänomene studieren.

Literatur