Zufallszahlen aus dem Computer?

Das, was ein Computer berechnet, sollte natürlich nicht zufällig sein. Die sog. Zufallszahlen aus einer Programmierumgebung sind meist sog. Pseudo-Zufallszahlen. Sie verhalten sich in vielerlei Hinsicht wie wirkliche Zufallszahlen und sind für numerische Analysen gut geeignet. Eine bekannte Methode, welche Zufallszahlen benutzt, ist die Monte-Carlo-Methode. Ich benutze Zufallszahlen zum Beispiel, um Sterne in Ansammlungen wie Galaxien zu verteilen, und dann damit weiterzurechnen.

Die Rechenalgorithmen erzeugen in der Regel Ganzzahlen. Diese lassen sich jedoch ziemlich einfach in Zahlen zwischen 0 und 1 umwandeln, und so benutze ich diese Zahlen auch. In Python erledigt dies die Funktion random(), die Zahlen sind gleich zwischen 0 und 1.
Die so erzeugte Zahlen nennt man gleichverteilt, weil das Intervall zwischen 0 und 1 gleichmäßig mit solchen Zahlen belegt wird. Man kann sich ein kleines Programm schreiben, was dies demonstriert: Man teilt den Bereich in 10, 100 oder 1000 Intervalle (Teile), erzeugt ein paar Tausend Zufallszahlen und schaut nach, wie sich diese Zahlen auf die Intervalle aufteilen. Das ist dann einigermaßen gleichmäßig. Natürlich nicht völlig; denn der Zufall spielt immer mit. Ein Beispiel in Python:


from random import *

l=[0,0,0,0,0,0,0,0,0,0] # Liste mit 10 Spalten

for i in range (1000): # 1000 Zufallszahlen erzeugen
    index=int(10*random()) # aus der ZZ eine Ganzzahl [0..9] herstellen
    l[index]=l[index]+1
for i in range (10):
    print (i, l[i])

Ungleich verteilt, wozu?

Für die meisten Anwendungen ist das Intervall [0, 1] ungeeignet. Durch Multiplikation mit einem Faktor und ggf. nach Addition eines Summanden kann man ganz schön viele Anwendungsfälle abdecken. Manchmal muss es aber sein, dass die Zufallszahlen im Intervall ungleich verteilt sind, z.B. an einer Seite dichter besetzt.

Ein Beispiel dazu: Für einige astronomische Anwendungen muss man eine Kugeloberfläche gleichmäßig dicht mit Zufallszahlen belegen. Aus solchen Kugelschichten kann man z.B. Kugelsternhaufenmodelle basteln oder die Koma eines Kometen (dazu habe ich es benötigt). In Kugelkoordinaten gerechnet hat man zwei Winkel, die ich mit λ und φ bezeichnet habe, analog den geographischen Koordinaten der Erde:

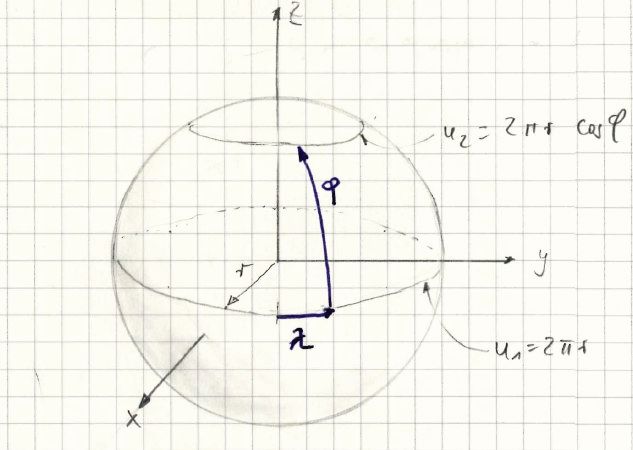
Wenn man die Kugel gleichmäßig bedecken möchte muss man beachten: Je größer φ wird, desto weniger Werte dürfen erzeugt werden, und zwar nach dem Kosinusgesetz. Man benötigt also Zufallszahlen mit einer Kosinusverteilung.

Die Verwerfe-Methode, ein statistisches Verfahren

Das Prinzip der Verwerfe-Methode: Zuerst wird ein Zufallszahlenkandidat erzeugt, bei uns wäre das ein Paar von Winkelkoordinaten. Die Verteilungsdichte an der Stelle des Kandidaten kennen wir ja. Es wir jetzt ermittelt, ob wir den Kandidaten annehmen wollen. Hierzu wird eine getrennte Zufallszahl erzeugt, und geschaut, ob sie kleiner als die gewünschte Dichte ist. Wenn ja, dann wird der Kandidat akzeptiert, ansonsten verworfen. Klingt kompliziert, deshalb erläutere ich das an einer Grafik:

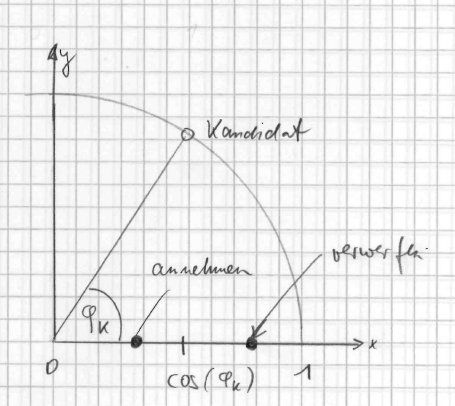
Die schwarzen Kreise sind die zweite Zufallszahl. Diese bewirkt:

Falls φ nahe Null und der Kosinus fast 1 ist, dann werden nahezu alle Kandidaten durchgelassen. Für diese Region werden also viele Ergebnisse erzielt.
Im mittleren Bereich von φ werden manchmal welche akzeptiert und manchmal welche verworfen.
Wenn wir nahe φ=90° kommen, dann wird es sehr schwer einen Kandidaten "durchzubekommen", es werden kaum noch Ergebnisse erzielt.

Die Verwerfemethode ist leicht zu implementieren, auch für komplizierte Verteilungen. Allerdings werden mehr Zufallszahlen erzeugt, als unbedingt nötig. Bei ungünstigen Verteilungen kann es recht lange dauern, ehe ein Kandidat "durchkommt", hier beim Kosinus geht es noch.

Ein Python-Programm dazu:

from random import *
from math import *

l=[0,0,0,0,0,0,0,0,0] # Liste mit 9 Spalten à 10 Grad

for i in range (2000): # 2000 Versuche
    winkel=int(90*random()) # Winkel 0...90°
    kosinus=cos(pi*winkel/180)
    if (random()<kosinus):
        index=int(winkel/10) # Scheiben zu 10°
        l[index]=l[index]+1
for i in range (9):
    print (i+1, l[i])

In der ersten Spalte, welche die Winkel zwischen 0 und 10 Grad abdeckt, sind etwa 10x mehr Treffer als in der letzten für die Winkel zwischen 80 und 90°. Das ist ja jedes Mal anders, weil es Zufallszahlen sind, hier aber eine Grafik:

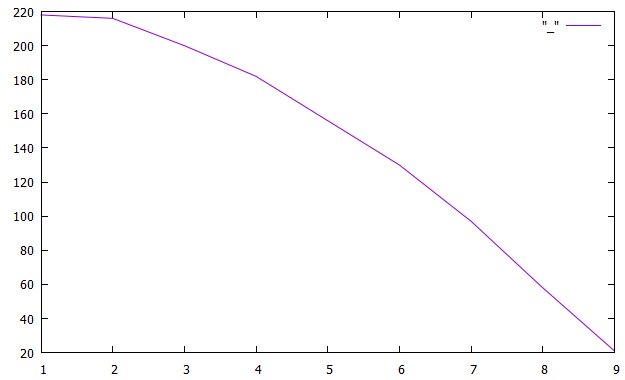
Die Inversionsmethode, rein analytisch

Die Inversionsmethode berechnet eine Funktion, durch die man die gleichverteilte Zufallszahl schicken muss, um die gewünschte Verteilung zu erhalten. Sie kann nur angewandt werden, wenn die gewünschte Verteilungsfunktion erst einmal überhaupt analytisch bekannt ist (und nicht selbst aus irgendeinem Näherungsverfahren kommt), und auch noch von der mathematischen Struktur nicht zu kompliziert ist. Zum Beispiel muss sie sich integrieren lassen. Ich erläutere das an unserem Beispiel.

Da ich hier über allgemeine mathematische Funktionen schreibe, setze ich x für den Winkel statt φ. Das macht die Anwendung auf andere Funktionen leichter. Ausgangspunkt ist die Häufigkeitsverteilung h, die bei uns proportional dem Kosinus des Winkels x ist:
    h ~ cos(x)
Diese verwandeln wir in eine richtige Funktion, also eine Formel, in dem wir das Proportionalitätszeichen durch einen Faktor a ersetzen:
    h = a · cos(x)
Diese Funktion wird integriert, die Ergebnisfunktion nennen wir z. Die Integrationsgrenzen werden durch den gewünschten Zielbereich vorgegeben. Aus x = 0 wollen wir die Zufallszahl 0 Grad erhalten, und für x=1 soll die ungleich verteilte Zufallszahl den Wert 90 Grad haben
    z = a · ∫ cos(x)
    z = a · sin(x) + C

C ist die Integrationskonstante. Durch Einsetzen der Integrationsgrenzen können a und C berechnet werden. Die untere Integrationsgrenze muss den Wert 0 ergeben, weil unsere Zufallszahlen ab 0 beginnen. Die obere Grenze muss den Wert 1 ergeben, weil die gleichverteilten Zahlen mit 1 enden
0 = a · sin(0°) + C : C = 0
1 = a · sin(90°) + 0 : a=1

Die Zielfunktion für z ist demnach
z = sin(x)

Diese Funktion muss nun invertiert werden. Selbst wenn sich die Funktion integrieren lässt, kann sie nicht immer auch invertiert werden. Hier geht das aber:
x = arcsin(z)

Wenn wir eine gleichverteilte Zufallszahl durch den Arcus Sinus jagen, erhalten wir eine Kosinus-verteilte Zufallszahl. Ein Python-Programm hierzu:

from random import *
from math import *

l=[0,0,0,0,0,0,0,0,0] # Liste mit 9 Spalten à 10 Grad

for i in range (1000): # 1000 Zufallszahlen
    x=asin(random())
    x=180*x/pi; # in Gradmaß umrechnen
    index=int(x/10) # Scheiben zu 10°
    l[index]=l[index]+1
for i in range (9):
    print (i+, l[i])

Die grafische Ausgabe ist identisch derjenigen der Verwerfe-Methode.

Die Inversions-Methode ist für die Durchführung der Rechnung die wirtschaftlichste. Es werden nur soviele Zufallszahlen erzeugt, wie tatsächlich auch benötigt werden. Die allgemein verwendeten Algorithmen für solche Zufallswerte sind zwar schnell; das ändert sich aber, wenn man hochwertige Zufallszahlen benutzen muss, an deren Güte hohe Anforderungen gestellt werden. Moderne Programiersprachen wie C++ bieten hierfür zahlreiche Varianten für unterschiedliche Anwendungszwecke.
Bei mir ist es schon vorgekommen, dass ich für eine Simulation mehrere Milliarden Zufallszahlen benutzt habe, eben für eine hihe Genauigkeit. Da lohnt es sich, eine wirtschaftliche Methode zu benutzen.

(Uwe Pilz, Januar 2019)