Wie hängt der wahrgenommene Komadurchmesser eines Kometen mit der gemessenen Gesamthelligkeit zusammen?

Kometen sind meist sehr diffus und erfordern einen transparenten Himmel. Wenige Zehntel Magnituden an visueller Grenzgröße können den wahrgenommenen Komadurchmesser erheblich beeinflussen. Wir haben versucht, dieses Problem einmal vom theoretischen Standpunkt her zu bearbeiten.

Das Modell des freien Abströmens

Die Oberflächentemperatur gibt den Gasteilchen des Kometen eine kinetische Energie mit. Diese erzeugt die mittlere Abströmgeschwindigkeit von einigen hundert Metern in der Sekunde. Wenn sich der Komet in einem quasi-stationären Zustand befindet, sich also weder die Oberflächentemperatur noch die Produktionsrate merklich ändern, dann strömen in jeder Zeiteinheit dieselbe Menge Gasteilchen von einer kugelförmigen Hülle um den (als kugelförmig angenommenen) Kometen. Dies führt dazu, dass in jeder Kugelschale gleich viele Teilchen enthalten sind.
Da der Staub vom Gas mitgerissen wird, hat auch dieser nach einer kurzen Beschleunigungsstrecke eine feste Geschwindigkeit. Für die Staubanteile gilt demnach dasselbe Modell, wenngleich sich der Staub insgesamt langsamer bewegt.

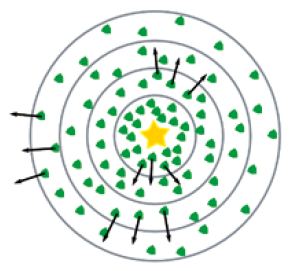
Das freie Abströmen von Gas und Staubteilchen bewirkt, dass in jeder gleich dicken Kugelschale der Koma gleich viele Teilchen liegen.

Dieses dreidimensionale Gebilde wird nun bei der Beobachtung auf den Himmelshintergrund projiziert. Um diese Projektion zu berechnen, bedienen wir uns des Kugelschalenmodells.

Das Kugelschalenmodell

Um die Projektion der Koma auf den Hintergrund numerisch oder analytisch zu simulieren, liegen zwei Herangehensweisen auf der Hand

Die Koma wird gedanklich in unendlich dünne Schichten zerlegt. Die Projektion ist das Integral über diese Schichten – das Differentialmodell.
Die Koma wird in Schichten mit einer merklichen Schichtdicke zerlegt. Die Projektion ist Die Summe über diese Schichten – das Kugelschalenmodell.

Vom rein mathematischen Standpunkt aus ist der erste Ansatz genauer. Er enthält aber ein schwer lösbares Problem: Die Teilchendichte steigt zum Nukleus des Kometen stetig an und ist genau im Inneren unendlich hoch. Darüber lässt es sich schwer integrieren, sowohl mathematisch als auch numerisch. Wir haben uns deshalb für das Kugelschalenmodell entschieden, was diese Singularität umgeht:

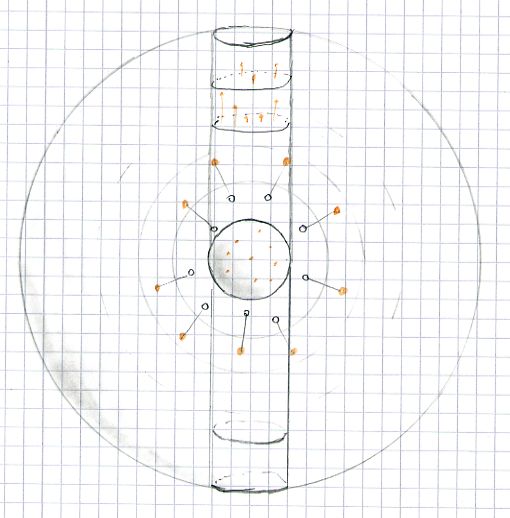
Mit dem Kugelschalenmodell kann die projizierte Dichte berechnet werden, in dem Teilchen summiert werden, welche sich in einem Zylinder befinden, der durch die Kugel im Zentrum läuft.

Die Verdichtung des dreidimensionale Gebildes auf den Himmelshintergrund projiziert führt visuell zu einer Verdichtung der inneren Koma. Es ist ein Ziel dieser Rechnungen und Simulationen, den Verlauf der Flächenhelligkeit zu berechnen.

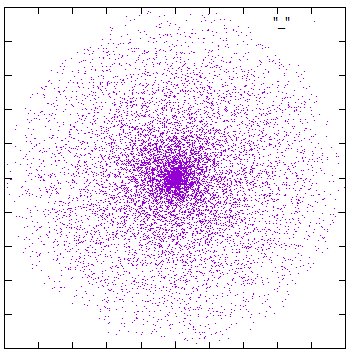
Simulierte Kometenkoma, es wurden 10 Schalen berücksichtigt

Nimmt die Dichte der Koma immer weiter zu, wenn man immer mehr Schalen berücksichtigt?

Das Modell des freien Abströmens hat einen gravierenden Makel: Gemäß diesem Modell überschreitet der Komadurchmesser jedes Maß, und wird unendlich groß. Die Frage: Genügt es, nur den inneren Teil zu berücksichtigen, und wenn ja, wie weit muss man da gehen?

Zuerst die Antwort: Für die Dichte im Zentrum genügt es, je nach Genauigkeitsanspruch, 10 bis 100 Schalen zu berücksichtigen.

Zur Begründung schauen wir uns die Dichte im zentralen Zylinder wie im Bild oben an. Das ist ja die Maximaldichte, also diejenige der projizierten Umgebung des Nukleus. Als erstes ein Ausflug zum Differentialmodell: Hierbei summieren wir den Zylinder aus unendlich dünnen Schichten. Um die Unstetigkeit ganz im Inneren des Modells zu beseitigen und andere Probleme zu umgehen, führen wir diese Simulation erst ab einem gewissen Abstand vom Zentrum durch, z.B. ab der 10. Schale. Unterhalb dieser Schale liegt eine feste Anzahl Teilchen im Zylinder. Um die Frage zu beantworten, on die Teilchenanzahl über jedes Maß wächst, je mehr Schalen wir berücksichtigen, können wir diese feste Anzahl ignorieren – auch wenn wir sie nicht kennen.

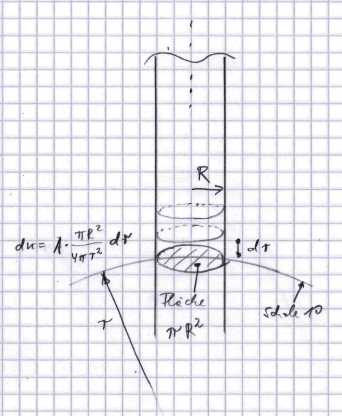
In einem größeren Abstand vom Nukleus machen wir keinen großen Fehler, wenn wir den "Deckel" des Zylinders als flach ansehen. Genaugenommen ist er gewölbt, aber diese Wölbung wird immer geringer, je weiter wir nach außen kommen. In der 10. Schale ist er schon ganz schön flach. Dann hat dieser "Deckel" eine feste Fläche, und der Zylinder wird aus feinen Scheiben mit sehr kleiner (genau unendlich feiner Dicke) aufgebaut. Die (auch unendlich dünne) Kugelschale, zu der jeder dieser dünnen Deckel gehört, wächst aber quadratisch mit dem Abstand vom Nukleus. Jede Kugelschale ist mit einer festen Anszahl von Teilchen besetzt, das ist ja gerade das Kugelschalenmodell. Der Zylinderdeckel entnimmt dieser Schale eine feste Fläche und damit einen kleinen Anteil dn der Gesamtteilchen der Schale, welche umgekehrt proportional der Entfernung r vom Nukleus ist:
    dn ~ 1/r² •dr oder dn = f • 1/r² • dr,
Hier ist dr winzig kleine Dicke des Zylinderdeckels und f ein Proportionalitätsfaktor, der von der der Teilchenanzahl in einer Schale sowie der Größe des Zylinders und damit von der Größe der inneren Kugel abhängt. Die Gesamtzahl der Teilchen in solch einem Zylinder lässt sich durch Integration ermitteln:
    n = f •∫ 1/r² dr
    n = f • 1/r [r_i, ∞]   n = f/r_i
Die Gesamtzahl ist also begrenzt.

Die Teilchenzahl im zentralen Zylinder

_{Volker hat diese Gesamtzahl der Teilchen im zentralen Zylinder mit dem Schalenmodell
nun wirklich berechnet, und zwar durch die exakte Berechnung von
Volumenintegralen. Hier ist seine "geniale" Rekursionsformel:}

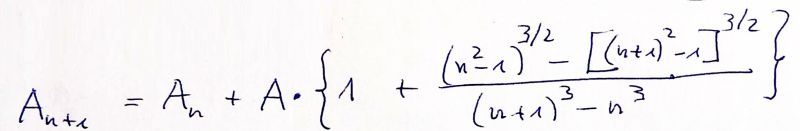
Hierin ist A_n die Anzahl der Teilchen des Zylinderausschnitts von ganz innen bis zur Schale Nummer n. Der Wert A ist die Anzahl der Teilchen der inneren Kugel und damit gleich der Gesamtzahl der Teilchen, die in jeder Schale vorhanden sind. Der Ausdruck in den geschweiften Klammern gibt also an, welchen Anteil dieser Teilchen der Zylinder aus der Schale mit der Nummer n+1 ausschneidet. All diese Anteile summiert geben also die Teilchenanzahl im gesamten Zylinder, und diese geben dann die Leuchtdichte des Kometen an dieser zentralen Stelle. Volker hat berechnet, das sich diese Summe dem Wert 1,506...-fachen von A, also der Teilchenzahl in der Kugel, nähert.

Ich (Uwe) habe ein kleines Python-Porgramm geschrieben, was die ersten Schalensummen ausgibt und dann noch einmal die Millionste. Wie meine Überlegungen am Differentialmodell zeigen, ist der Restfehler dabei im Bereich von 1:1 Mio.

	
A=1
A1=A
n=1
for i in range(10):  # die ersten 10 ausgeben
    print (n,A)
    A=A+A1*(
        1 + ( (n*n-1)**1.5 -((n+1)**2-1)**1.5 ) /
            ( (n+1)**3-n**3 )
        )
            
    n=n+1
   
for i in range(999989): # bis 1 Mio nur rechnen ...
    A=A+A1*(
        1 + ( (n*n-1)**1.5 -((n+1)**2-1)**1.5 ) /
            ( (n+1)**3-n**3 )
        )           
    n=n+1
print (n,A) # .. und am Schluss ausgeben

Nach 1 Mio. Schalen ergibt das Programm den Grenzwert 1.506480, in Übereinstimmung mit Volkers Angabe.
Ich habe ein Teilchen-Simulationsprogramm geschrieben, was diese Schalen mit Zufallsteilchen belegt und den Zylinderinhalt durch Auszählen ermittelt. Das Ergebnis stimmt für alle praktischen Zwecke mit Volkers theoretischem Ansatz überein. Es gibt eine kleine Abweichung innerhalb der ersten Schalen, die wahrscheinlich von kleinen Unterschieden im mathematischen Ansatz herrührt. Mein Grenzwert liegt bei 1,5706 für sehr große Teilchenanzahlen, also 4% Abweichung.

Beide Modelle, dass analytische und die numerische Simulation stimmen in den äußeren Schalen mit dem Differentialmodell überein.

Teilchenanzahlen in den Kreisringen

Mit einer ganz einfachen Überlegung kam Volker zu der Erkenntnis, dass in jeder projizierten Kugelschale genau so viele Teilchen liegen wie im mittleren Zylinder = dessen projizierter Kreisscheibe. Für diese Überlegung benutzen wir den Wert γ = 1,506...

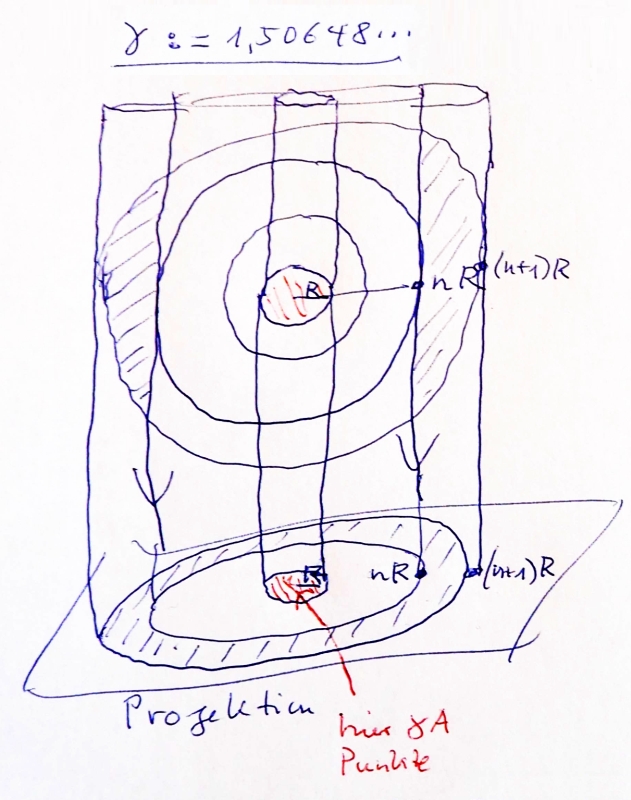
Der Fakt, dass ein Zylinder das γ-fache der Teilchen in der zentralen Kugel enthält, gilt ja für Zylinder beliebiger Größe. Ein doppelt so großer Zylinder hat als Ausgangspunkt eine doppelt so große Kugel in der Mitte. Wegen des Kugelschalenmodells ist diese Kugel genau eine Schale dicker als der Ursprungskugel, und enthält somit doppelt so viele Teilchen, Demnach enthält ein doppelt so dicker Zylinder eben auch doppelt so viele Teilchen wie der innere, ein dreifach so dicker dreimal so viele. Es folgt daraus durch Differenzbildung, dass jeder Kreisring dieselbe Anzahl Teilchen enthält.

Obwohl es daran kaum Zweifel geben kann, habe ich das mit 10 Mio. Teichen und 1000 Schalen simuliert – bis zu unendlich Schalen komme ich ja nicht. Die inneren 100 Schalen enthielten auch etwa gleich viele Teilchen, im Rahmen der Zufallsstreuung wieder.

Auf Magnituden umgerechnet bedeutet das: Wenn m₀ die Magnitude der kleinsten Apertur a₀ ist, dann ist die Magnitude m einer beliebigen Apertur a

m = m₀ - 2,5 log (a/a₀)

Ich habe die Ergebnisse dieser Formel in die Grafik eingetragen, welche sehr genaue Messungen für den Kometen 46P/Wirtanen von Anfang Dezember 2018 enthält. Die Messungen wurden von Thomas Lehmann und Steffen Fritsche ausgeführt:

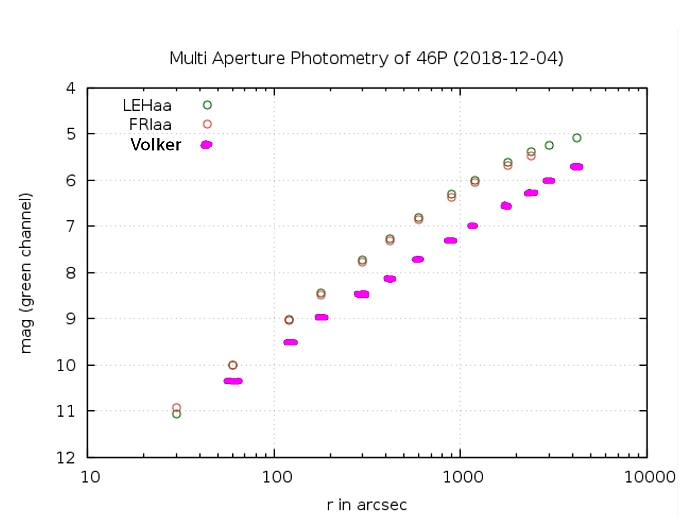
Man sieht zweierlei:

Die Messungen von Thomas und Steffen stimmen sehr gut überein.
Der beobachtete Helligkeitszuwachs über der Apertur ist stärker als vom Modell des freien Abströmens vorhergesagt.

Der zweite Punkt ist unerwartet: Ich hatte schon damit gerechnet, dass das Magnetfeld und der Sonnenwind die Koma ausdünnen. In Wirklichkeit haben wir es aber nicht mit einem freien, sondern mit einem gebremsten Abströmen zu tun: Stoff zum Nachdenken, und auch dazu, neue Modelle zu entwerfen.

(Volker Kasten und Uwe Pilz, Januar 2019)