Startseite  | Programm-Archiv | Analyse Luftdichte, höhenabhängig | Unsere Vorläufer | Kontakt, Datenschutz

Der Luftdichte in verschiedener Höhe

Wenn man die Bewegung von Körpern durch die Erdatmosphäre berechnet möchte, benötigt man den die Dichte der Luft, da sich die Bremswirkung erhöht, wenn die Dichte zunimmt. Astronomische Beispiele für solche Körper sind Meteore bzw. Meteorite und Raumflugkörper beim Wiedereintritt.

Die Dichte der Atmosphäre erhöht sich, von außen kommend, exponentiell. Der Grund dafür ist, dass die Luft komprimierbar ist. Zur Erde zu hat man nicht nur mehr Luftmassen übersich, sondern zunehmend dichtere. Auf dieser Seite möchte ich Formeln angeben, mit dennen sich diese Dichte-Abhängigkeit unkompliziert berechnen lässt.

Vie benutzt wird sog. U.S. Standard-Atmosphäre von 1976 . Ich gebe die Tabelle hier an:
  h(m)   T(°C) g(m/s²) ρ(kg/m³)
  -1000  21.50 9.810 1.347
      0  15.00 9.807 1.225
   1000   8.50 9.804 1.112
   2000   2.00 9.801 1.007
   3000  -4.49 9.797 0.9093
   4000 -10.98 9.794 0.8194
   5000 -17.47 9.791 0.7364
   6000 -23.96 9.788 0.6601
   7000 -30.45 9.785 0.5900
   8000 -36.94 9.782 0.5258
   9000 -43.42 9.779 0.4671
  10000 -49.90 9.776 0.4135
  15000 -56.50 9.761 0.1948
  20000 -56.50 9.745 0.08891
  25000 -51.60 9.730 0.04008
  30000 -46.64 9.715 0.01841
  40000 -22.80 9.684 3.996e-3
  50000 -2.5   9.654 1.027e-3
  60000 -26.13 9.624 3.097e-4
  70000 -53.57 9.594 8.283e-5
  80000 -74.51 9.564 1.846e-5

Ich habe die Dichte dieser Tabelle durch eine Ausgleichsrechnung angenähert:

log(ρ) = 6.07149e-5 · h +0.1113988

Hiermit kann man die Dichte bis in 100 oder vielleicht auch 150 km Höhe gut abbilden.

~

In der Wikipedia ist eine Grafik gegeben, welche die Luftdichte ebenfalls darstellt. Die Quelle Allgemeine Meteorologie Nr. 1, Selbstverlag des Deutschen Wetterdienstes, Offenbach, 1987, ist mir leider nicht zugänglich, ich musste die Daten aus dem Diaggramm entnehmen. Diese Quelle berücksichtigt die äußere Atmosphäre jenseits von 200 km Höhe. Dort draußen fällt dic Dichte langsamer ab als in den inneren Atmosphärenschichten.

Im Original ist die Luftdichte die unabhängige Variable, daraus kann die Höhe berechnet werden. Die Frage hier ist anders: In welcher Höhe herrscht welche Luftdichte? Ich habe deshalb die Kurve gedreht:

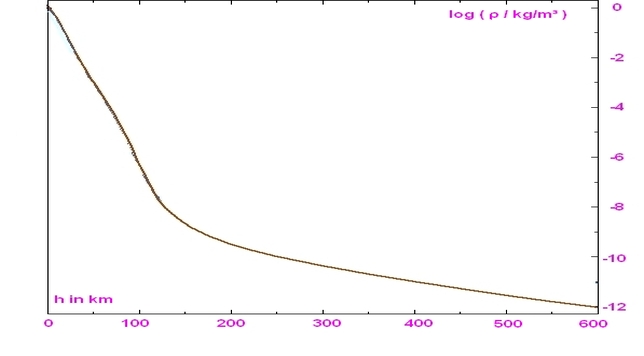
Die Dichte ist hier als Logarithmus angegeben. 0 bedeutet ρ=10⁰ kg/m³, also etwa 1 kg/m³ – in etwa der Wert in Bodennähe. In 100 km Höhe ist das schon etwa 10^-8 kg/m³, also nur noch 10 µg/m³. Dennoch ist das so hoch, dass es Satelliten beeinflusst. Stabile, langfristige Bahnen sind erst ab etwa 200 km Höhe möglich.

Für die Benutzung in einem Computerprogramm muss man dies irgendwie in eine Formel bringen. In geschlossener Form ist das schwer. Ich habe die Kurve deshalb in drei Abschnitte unterteilt:

• Bis 100 km kann man den Zusammenhang durch eine Gerade annähern
• oberhalb von 250 km kann der Zusammenhang durch eine andere Gerade beschrieben werden
• den gekrümmten Übergangsbereich habe ich durch ein Polynom dritten Grades angenähert

Die Formeln (Höhe h jeweils in km einsetzen):

• bis 100 km: Log (ρ) = -0,0643 h
• 100 - 250 km: Log (ρ) = -1,4865 · 10^-6 · h³ + 9,642 · 10^-4 · h² - 0.216275 · h + 7,000
• ab 250 km: Log (ρ) = -0,005714 · h -8,571

Ich habe ein kleines Python-Programm geschrieben, was diese Formel enthält und eine Liste zwischen h=0 und h=600 m ausgibt. Hieraus kann man eine Grafik herstellen:

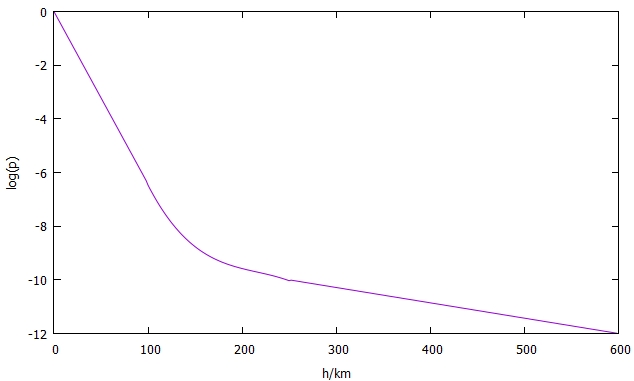
Ein kleiner Knick ist zu sehen beim Übergang vom Polynom auf die großen Höhen, aber insgesamt sieht es ganz brauchbar aus. Zum Schluss noch das Python-Programm:

# Funktion für die Luftdichte
from math import *

def luftdichte(h):
    if h<100: return-0.064301*h
    if h>250: return -0.0057144*h-8.571
    return -1.4865e-6*h*h*h+9.642e-4*h*h-0.216275*h+7

# eine Liste ausgeben
h=0
for i in range (300):
    print(h, luftdichte(h))
     h=h+2