Partielle Differentialgleichungen

Die Ungleichheit
ist die Ursache aller örtlichen Bewegungen.
Leonardo da Vinci

Einführung

Differentialgleichungen sind Funktionen – sie beschreiben den Zusammenhang zwischen zwei oder mehreren Größen. Ich habe hierzu einen Einführungsaufsatz hinterlegt, welche die sog. gewöhnlichen Differentialgleichungen beschreibt.

Partielle Differentialgleichungen entstehen aus mathematischen Modellen für physikalische Vorgänge, welche von mehreren Variablen abhängen. Diese Variablen sind fast immer der Ort und oft auch die Zeit. Ein Beispiel dafür ist die Wärmeleitung in einem Körper oder auch in einem nicht begrenzten Volumen. Die gesuchte Größe ist die Temperatur, welche vom Ort abhängt und auch von der Zeit abhängen kann.

Eine als partielle Differentialgleichung formuliertes Modell macht Aussagen über die Änderungen der gesuchten Größe, wenn sich die unabhängigen Variablen (z.B. Ort und Zeit) ein ganz klein wenig ändern – genau genommen nur ein unendlich kleines Stück. Diese Formulierung ist meist nicht besonders schwierig. Problematisch ist es, eine Aussage über die gesuchte Größe in der gesamten Region und über die gesamte betrachtete Zeit zu bekommen. Nur in ganz einfachen Fällen ist dies Formelmäßig möglich.

Die Beschreibung der lokalen und zeitlichen Änderungen definiert das Problem nicht vollständig, sondern eben nur das physikalische Geschehen. Ein vollständig beschriebenes Problem benötigt Randbedingungen für den Ort und Anfangsbedingungen für die Zeit. Beispiel: Die Berechnung der Temperaturverteilung in einem Zylinder und deren zeitliche Änderung erfordert:

Den Verlauf der Temperatur oder des Wärmeflusses am Rand
Die Anfangswerte der Temperatur im Volumen
ggf. die Angabe von Wärmequellen

Es können auch kompliziertere Anfangsbedingungen gegeben sein.

Ein numerisches Herangehen könnte darin bestehen, die unendlich kleinen Änderungen durch endlich große Differenzen zu ersetzen. So könnte man für das Beispiel den Quader in einige Tausend kleine Würfel teilen und die Zeit in millisekundenweise voranschreiten lassen. In einem der kleinen Quader wird die Temperatur als konstant angenommen und ändert sich erst nach Ablauf eines kleinen Zeitschrittes.

Die Wärmleitung ist von der numerischen Zugänglichkeit besonders einfach. Nach den mathematischen und numerischen Schwierigkeiten und den damit verbundenen Lösungsstrategien werden partielle Differentialgleichungen in drei Klassen eingeteilt, sog. elliptische, parabolische und hyperbolische Probleme. Dieser Aufsatz soll diese Typen und ihre Eigenschaften beleuchten.

Elliptische Differentialgleichungen

Elliptische Differentialgleichungen beschreiben zeitlich unveränderliche Prozesse. Beispiele dafür

das Gravitationspotential bei gegebener Masseverteilung
Temperaturverteilung eines Körpers (z.B. eines Sterns) im thermischen Gleichgewicht
die wirbelfreie inkompressible Strömung, z.B. die Konvektionsströmung im Inneren eines Sterns (vereinfacht)

Das Problem benötigt zur vollständigen Beschreibung Randbedingungen. Die wichtigsten beiden sind:

Die Verteilung der zu berechnenden Größe (z.B. der Temperatur) ist am Rand gegeben – sog. Dirchichletsche Randbedingungen
Die Änderung der zu berechnenden Größe senkrecht zum Rand ist gegeben (z.B. der Wärmefluss durch einen Rand ist gegeben, oft ist das Null) – Neumannsche Randbedingung

Eine elliptische Differentialgleichung hat die typische Form

Hierbei ist Q die betrachtete Größe (z.B. die Temperatur), und ' bedeutet eine Ableitung nach dem Ort. Die erste Ableitung ist bei nur einer Unabhängigen der Anstieg, die zweite Ableitung ist die Änderung des Anstiegts, welche man vielleicht Wölbung nennen könnte. Bei mehreren Unabhängigen (z,B. im Raum mit drei Ortskoordinaten) ist die erste Ableitung der Gradient, das ist ein Vektor, welcher die Richtung des stärksten Anstiegs angibt. Die zweite Ableitung heißt Divergenz und wird auch als Quellendichte bezeichnet.

Die Richtung des stärkten Anstieges ist meist mit einer Art Strömung verbunden. Das kann die wirkliche Strömung einer Flüssigkeit sein, ein elektrischer Strom, ein durch Diffusion bewegter Teilchenstrom oder die Strömung von Wärme. Die elliptische Differentialgleichung besagt nun, dass dieser Strom das Lösungsgebiet "glatt" durchließt, ohne das irgendwo etwas hineingespritzt oder abgesaugt wird. Dieser Strom kann sich übrigens auch nicht "im Kreis herum" bewegen, das geht nicht, wenn man sich immer in Richtung des stärksten Anstieges bewegt: Ein Gradientenfeld ist quellenfrei.

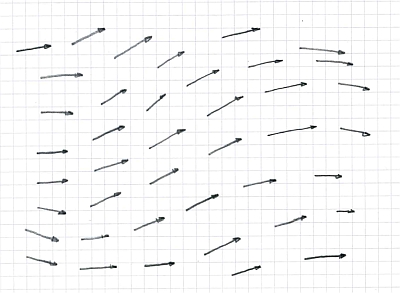
Das Gradientenfeld einer elliptischen Differentialgleichung enthält keine Quellen oder Senken.

Im eindimensionalen Fall hängt die gesuchte Größe nur von einer Ortskoordinate ab. Im einfachsten Fall verändern sich weder die Stoffwerte noch der Querschnitt: Dann hat die gesuchte Größe einen linearen Verlauf.

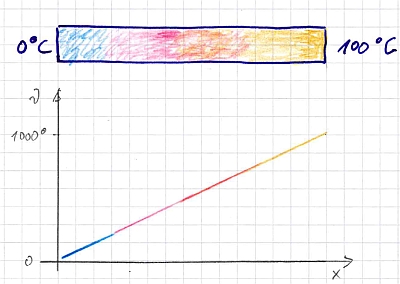
Die Wärmeleitung ohne Wärmequellen wird durch eine elliptische Differentialgleichung beschrieben. Die Wärmeleitung durch einen am Umfang isolierten Stab ist eindimensional. Die Temperatur muss sich dann linear verändern – das ergibt sich aus der Differentialgleichung.

Ein Lösungsansatz für komplexe Fälle besteht darin, das Lösungsgebiete in kleine Teile aufzuspalten und für diese Teiler vereinfachte Annahmen zu machen – z.B. dass die gesuchte Größe in den kleinen Raumgebieten jeweils konstant ist. Dann führt die Lösung auf ein lineares Gleichungssystem. Dies bietet sich z.B. für die Temperaturverteilung an.

Parabolische Differentialgleichungen

Parabolische Differentialgleichungen beschreiben ähnliche Effekte wie die elliptischen, aber im instationären Fall. Beispiel ist der zeitliche Verlauf der Temperatur in einem thermisch isolierten Körper, der im Inneren an einer Stelle erhitzt wurde. Diese Störung des Gleichgewichts verteilt sich mit der Zeit im Raum und gleicht sich aus, im Laufe der Zeit werden die Änderungen der betrachteten Größe immer geringer.

Eine parabolische Differentialgleichung hat die typische Form

Q ist wieder die betrachtete Größe, c ist eine Konstante. Mit dem Punkt über dem Buchstaben wird eine Zeitableitung gekennzeichnet. Das heißt, die Divergenz = Quellendichte führt zu einer zeitlichen Änderung, die man als Ausbreitungsgeschwindigkeit interpretieren kann. Der Gradient wird allmählich über das Lösungsgebiet verteilt: Unregelmäßigkeiten im Gradientefeld werden immer geringer, scharfe Gradienten verschleifen und und die Lösung nähert sich einem stationären Zustand.

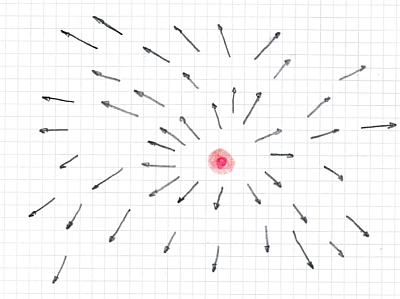
Das Gradientenfeld einer parabolischen Differentialgleichung enthält Quellen und Senken.

Für parabolische Differentialgleichungen müssen wie bei der elliptischen Differentialgleichung Randwerte vorgeschrieben werden. Außerdem benötigt die Problembeschreibung zeitliche Anfangswerte.

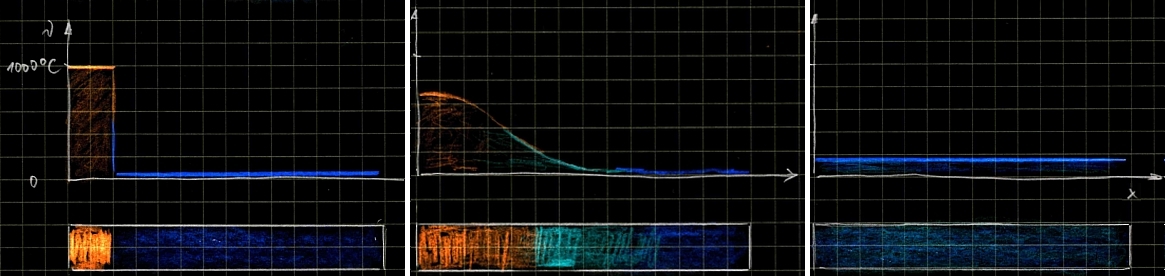
Dargestellt ist der Temperaturausgleich eines isolierten Stabes, der an einem Ende kühler ist. Ein solcher Ausgleich folgt einer parabolischen Differentialgleichung.

Ein Lösungsansatz besteht darin, dass Lösungsgebiet wie bei elliptischen Differentialgleichungen in kleine Teile zu spalten und deren zeitliche Entwicklung zu verfolgen. Dafür muss auch die Zeit in Schritte geteilt werden. Für die Änderung während eines Zeitschritts werden vereinfachende Annahmen getroffen, z.B. die Änderungsrate bleibt für einen Zeitschritt konstant.

Hyperbolische Differentialgleichungen

Wellengleichungen nennt man hyperbolisch. Wie die parabolischen Differentialgleichungen sind sie zeitabhängig. Allerdings verteilt sich bei diesen Problemen eine Störung nicht im Raum, sondern sie wandert mit unveränderter Stärke durch den Raum – eben eine Welle. Oder anders ausgedrückt: Die Lösung ist nur so glatt wie die Anfangsbedingungen, scharfe Änderungen der untersuchten Größen bleiben erhalten und pflanzen sich im Raum fort. Ein Beispiel sind Schock- und Stoßwellen, welche durch eine Supernova ausgelöst werden und im umgebenden Gas zu Verdichtungen führen. Aber auch Erdbeben folgen solchen Gleichungen.

Die typische Form hyperbolischer Differentialgleichungen ist

Ähnlich wie bei parabolischen Differentialgleichungen führt eine Quellendichte zu einer zeitlichen Änderung. In diesem Fall ist das aber keine Ausbreitungsgeschwindigkeit, sondern eine Beschleunigung. Dies führt dazu, dass ein anfangs vorhandender Gradient prinzipiell erhalten bleibt, sich aber räumlich fortsetzt, eine Welle also. Aus diesem Grund wird die obige Form auch Wellengleichung genannt.

Wie bei parabolischen müssen für hyperbolische Differentialgleichungen Randwerte und zeitliche Anfangswerte vorgeschrieben werden. Zusätzlich muss die zeitliche Änderung der gesuchten Größe (also eine Art Geschwindigkeit) als Anfangswert gegeben sein.

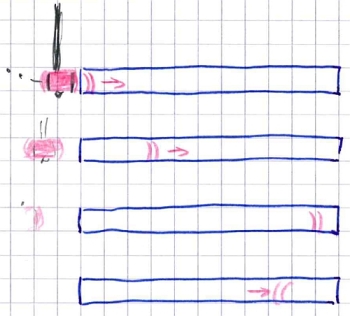
Ein Verdichtungs-Stoß in einem Stab pflanzt sich längs des Stabes fort und wird an den Enden reflektiert.

Ein Verfahren zu Lösung ist die explizite Zeitintegration. Das Raumgebiet wird durch Berechnungspunkte (Stützpunkte) repräsentiert, die Zeit schreiten schrittweise voran. Die die Differentialgleichung wird auf eine Differenzengleichung zurückgeführt und im Raum punktweise berechnet. Für jeden dieser Stützpunkte wird dann die Zeitableitung ebenfalls durch einen Differenzausdruck angenähert und die Lösung für den nächsten Zeitschritt berechnet.

(Uwe Pilz, Januar 2020)