Was sind Differentialgleichungen?

Die gerade Linie ist gottlos.
Friedensreich Hundertwasser

Vorwort: Gleichungen und Funktionen

Eine Gleichung stellt – wie der Name sagt – eine Gleichheit zweiter Ausdrücke fest, z.B.

        x²+2x=15

Hiermit kann man einen Ergebniswert für x ausrechnen, manchmal sind es auch mehrere einzelne Werte. Im Beispiel ist die Gleichung für x=-5 und x=3 erfüllt.
Funktionen hingegen stellen Zuordnungen zwischen zwei Größen auf, es können auch mehr als zwei Variablen sein. Ein Beispiel:

        y=x²

Wenn man einen Wert für x (die unabhängige Variable) auswählt, dann kann man ein y ausrechnen. Manchmal darf x nur einen gewissen Bereich durchlaufen (z.B. nicht negativ werden). Aber innerhalb dieses Bereiches ist jeder Wert zulässig und man erhält eine Kurve:

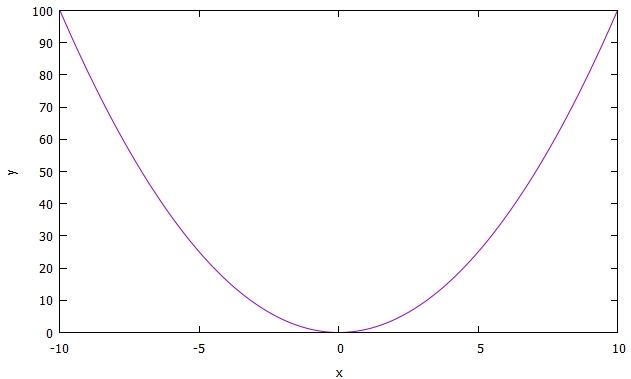
Kurve von y=x²

Es kann auch vorkommen, dass eine Funktion von zwei unabhängigen Größen abhängt, z.B.

        z = cos(x)*sin(y)

Hier sind x und y die unabhängigen Variable. Bei zwei unabhängigen Variablen kann man die Funktion noch in einer Art Schrägansicht darstellen. Bei noch mehr Variablen funktioniert das nicht mehr.

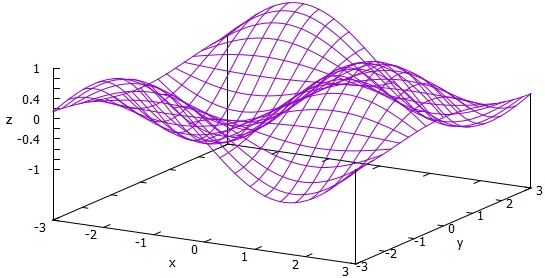
Kurve von sin(x)*cos(y)

Wenn man für alle unabhängigen Größen einen konkreten Wert einsetzt, dann wird aus einer Funktion eine Gleichung, und man kann den Funktionswert ausrechnen. Dies gelingt übrigens nicht für alle Gleichungen auf direktem Weg. Ein bekanntes Beispiel ist die Kepler-Gleichung:

        y- e*sin(y)=x

(hier in x und y geschrieben). Selbst wenn wir Exzentrizität e kennen und einen Wert für die unabhängige Variable x (das ist die mittlere Anomalie) haben, können wir die entstehende Gleichung nicht nach y auflösen und müssen uns etwas anderes einfallen lassen.

Und was sind nun Differentialgleichungen?

Differentialgleichungen sind keine Gleichungen (obwohl sie so heißen). Sondern es sind Funktionen, d.h. sie stellen Beziehungen zwischen zwei Variablen her. Ebenso wie bei normalen Funktionen können es auch mehr unabhängige Variablen sein. Die Funktion ist nun aber nicht direkt formelmäßig gegeben, sondern wird indirekt über ihre Eigenschaften beschrieben. In diesen Eigenschaften können vorkommen:

Ganz normale formelmäßige Ausdrücke
Glieder, welche neben x und y auch Ableitungen von y enthalten, also den Anstieg im Punkt x
Eine Randbedingung, welche die Werte von y für x für ein festes x festlegt

Den wirklichen formelmäßigen Zusammenhang kennt man zunächst nicht, und es gelingt auch nicht, die Kurve zu berechnen.
Als Beispiel habe ich die Geschwindigkeit eines Körpers gewählt, der z.B. in die Erdatmosphäre eintritt: Die Luft bremst diesen Körper ab. Wenn die Eintrittsgeschwindigkeit nicht sehr groß ist, dann ist íst die Bremskraft proportional zur Geschwindigkeit. Man kann eine Kräftebilanz aufstellen und daraus die Beschleunigung ausrechnen. Der Körper wird zwar langsamer, man sagt trotzdem Beschleunigung (die ist dann eben negativ):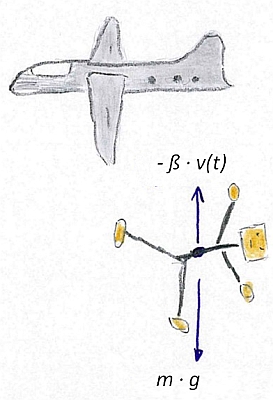

        m · a = m · g - β · v

    a ist die Beschleunigung
    v ist die Geschwindigkeit
    m ist die Masse des Teilchens
    g ist die Erdbeschleunigung
    β ist eine Konstante, welche die Bremswirkung beschreibt.

β hängt von der Form des Körpers ab und auch von der Dichte der Lufte. Man kann β aus Tabellenwerken entnehmen oder man kann den Wert für einen gegebenen Körper im Experiment bestimmen.

Wenn wir uns nun für den Verlauf der Geschwindigkeit im Verlauf der Zeit interessieren, dann müssen wir beachten, dass die Beschleunigung die erste Ableitung der Geschwindigkeit ist. Eine Formel für die Geschwindigkeit sieht dann also so aus:

m · v'(t) = m · g - β · v(t)

oder nach etwas umformen

v'(t) + β/m · v(t) = g

Die Geschwindigkeit ist von der Zeit abhängig, das habe ich jetzt mit hingeschrieben. v'(t) ist die erste Ableitung der Geschwindigkeit nach der Zeit, also die Beschleunigung.

Was wir jetzt wissen ist, dass die erste Ableitung der Geschwindigkeit plus irgendwas mal die Geschwindigkeit selbst gerade eben die Erdanziehungskraft ergeben soll. Einen ordentlichen formelmäßigen Zusammenhang zwischen v und t haben wir nicht. Das ist eben eine Differentialgleichung, da sie neben den Unbekannten selbst noch Ableitungen dieser Unbekannten enthält. In unserem Fall ist das nur eine Unbekannte und wir erhalten eine sogenannte gewöhnliche Differentialgleichung. Oft sind es mehrere Unbekannte, zum Besipiel alle Raumkoordinaten. Dann redet man von partiellen Differentialgleichungen.

Es ist unmittelbar einsichtig, dass uns die Lösung nicht durch eine einfache Formel für die Geschwindigkeit angegeben werden kann. Denn es gibt ja ganz unterschiedliche Verläufe der Geschwindigkeit, je nach dem, mit welcher Anfangsgeschwindigkeit das Teilchen eintritt. Wir benötigen diese Angabe zusätzlich, und das ist eine Randbedingung, hier konkret: Eine Anfangsbedingung.

Für diesen Fall gibt es eine formelmäßige Lösung, die ich ohne Herleitung einmal angebe:

        v(t) = v_∞ ( 1 - e^-t/τ) + v₀ e^-t/τ

    v_∞ ist die Endgeschwindigkeit nach sehr langer Zeit, es gilt v_∞ = m · g / β .
    v₀ ist die Anfangsgeschwindigkeit
    τ ist eine charakteristische Zeit, die kann mit τ = m / β berechnet werden.

Das "e" ist die Exponentialfunktion.

Ein Zahlenbeispiel

Ein Fallschirmspringer fällt vor dem Öffnen des Schirms einige Zeit im freien Fall. Für die übliche Körperhaltung "Arme und Beine weit gespreizt" haben wir näherungsweise die folgenden Eingangswerte:

        m=70 kg
        β = 15 kg/s

Daraus kann man die Endgeschwindigkeit und die Zeitkonstante bestimmen:

         v_∞ =46 m/s (etwa 160 km/h)
        τ = 4,7 s

Aus dem Flugzeug heraus ist die Anfangsgeschwindigkeit zunächst Null. Nach Ablauf von 4,7 s hat der Fallschirmspringer bereits 63% der Endgeschwindigkeit erreicht:

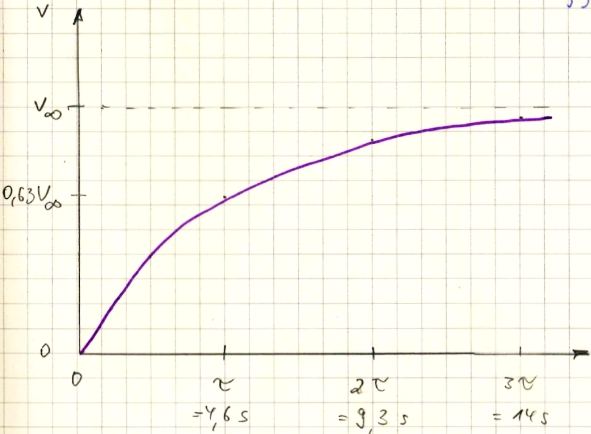
Geschwindigkeit eines Menschen im freien Fall

Nachbemerkung

Das Beispiel des freien Falls in der Luft gilt nur für kleine Geschwindigkeiten, bei der die Widerstandskraft proportional der Geschwindigkeit ist (Stokes'sche Reibung). Schon für den Menschen im freien Fall ist das nur noch eingeschränkt gültig.
Für den astronomisch interessanten Fall, nämlich, dass ein Meteor aufleuchtet, weil ein Körper mit hoher Geschwindigkeit die Erdatmosphäre trifft, gilt diese Annahme auf gar keinen Fall mehr. Die Kraft ist in diesem Fall vom Quadrat der Geschwindigkeit abhängig (Newton'sche Reibung). Aber auch dafür lässt sich eine Differentialgleichung aufstellen und lösen.

Wenn man allerdings berücksichtigen will, dass die Dichte der Luft bei Annäherung an die Erdoberfläche größer wird, dann ist z.B. im Fall der Stokes'schen Reibung β keine Konstante mehr, sondern ändert sich mit der Höhe. Für diesen, deutlich realitätsnäheren Fall lässt sich keine geschlossene (formelmäßige) Lösung mehr angeben. Man muss auf Näherungsverfahren zurückgreifen, die am besten mit Hilfe eines Computers benutzt werden.

(Uwe Pilz, Dezember 2018)