 Startseite
| Programm-Archiv
| Algorithmus
Runge-Kutta-Verfahren
|
Unsere Vorläufer
| Kontakt, Datenschutz
Startseite
| Programm-Archiv
| Algorithmus
Runge-Kutta-Verfahren
|
Unsere Vorläufer
| Kontakt, Datenschutz
 Startseite
| Programm-Archiv
| Algorithmus
Runge-Kutta-Verfahren
|
Unsere Vorläufer
| Kontakt, Datenschutz
Startseite
| Programm-Archiv
| Algorithmus
Runge-Kutta-Verfahren
|
Unsere Vorläufer
| Kontakt, Datenschutz
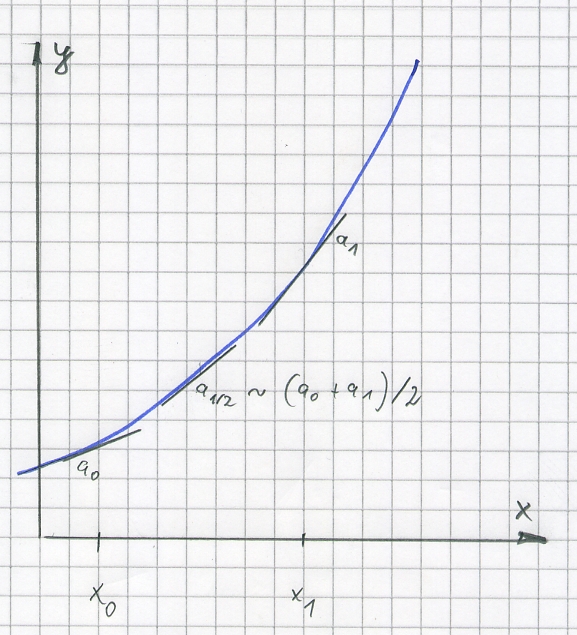
Beim einfachen Euler Cauchy-Verfahren wird der Anstieg am Anfang des Intervalls als repräsentativ angenommen. Dies ist sehr einseitig im wahren SInne des Wortes. Insbesondere bei monoton steigenden oder fallenden Anstiegen summieren sich diese Fehler schnell. Es wäre viel besser, den Anstieg in der Mitte des Intervalls zu benutzen, dieser repräsentiert. Das Verfahren nach Karl Heun benutzt hierfür einen Näherungswert, nämlich den Mittelwert aus den Anstiegen am Anfang und am Ende des Intervalls:
Dazu ist die Berechnung einer zusätzlichen Ableitung nötig am Ende des
Intervalls. Die Ableitungen
kosten aber in den meisten Fällen die meiste Rechenzeit. Dennoch lohnt sich
diese Investition, bei gleicher Rechenleistung wird eine viel höhere
Genauigkeit erzielt.
Die Berechnung des Anstieges am Ende des Intervalls
setzt voraus, dass wir x und y dort kennen, also x1
und y1 in der Skizze. x1 lässt sich leicht berechnen, y1ist
zunächst unbekannt. Deshalb wird y1 zunächst mit dem Euler-Cauchy-Verfahren
geschätzt (Vorhersage = Prädiktorschritt). Mit diesem geschätzten Wert wird
der mittlere Anstieg über das Intervall berechnet und damit die Vorhersage
verbessert (Korrektor-Schritt). Es gibt eine ganze Familie von sog.
Prädiktor-Korrektor-Verfahren, bei denen bereits berechnete Werte zur
Vorhersage noch unbekannter benutzt werden. Das Heun-Verfahren ist das
einfachste von ihnen.
Gegenüber dem Euler-Cauchy-Verfahren wird ein erheblicher Zuwachs an Genauigkeit erzielt. Beim einfachen Polygonzugverfahren benötigt man für eine 10-fahce Genauigkeit auch 10 mal mehr Stützstellen und damit die zehnfache Rechenleistung. Beim Heun-Verfahren ergibt eine 10-fach höhere Stützstellendichte die 100-fache Genauigkeit. Da spielt es dann kaum noch eine Rolle, dass der einzelne Rechenschritt zwei statt eine Auswertung des Anstieges benötigt.
# Heun-Verfahren
from math import *
# Konstanten
g=9.81
b=15
# Anfangsbedingungen
v=0
h=0
m=70
def beschleunigung(t, v, h):
# t und h werden hier nicht benötigt,
# aber die RK-Formel benutzt es
a=g
a=a-(b*v)/m
return a
# Hauptprogramm
dt=0.0001 # Zeitschritt
t=0
while t<20:
print(t, v)
h0=h # kopieren, damit die Formeln
v0=v # symmetrisch sind
# mit Euler-Cauchy einen Schritt vorwärts
# r1 und v1 mit a0, v0 berechnen
a0=beschleunigung(t, v0, h0)
h1=h0+v0*dt
v1=v0+a0*dt
# die Beschleunigung am Ende des Intervalls berechnen
a1=beschleunigung(t, v1, h1)
# daraus verbesserte Geschwindigkeit und Höhe
h=h+dt*(v0+v1)/2
v=v+dt*(a0+a1)/2
t=t+dt
Carl Runge und Martin Wilhelm Kutta entwickelten ein Verfahren, welches bei einer 10-fachen Erhöhung der Stützstellendichte gleich vier zusätzliche Stellen an Ergebnisgenauigkeit ergibt. Hierzu sind im Intervall vier Auswertungen des Anstiegs nötig. Das Runge-Kutta-Verfahren ist sehr genau und wird deshalb für praktische Anwendungen oft eingesetzt. Hier nur das Hauptprogramm, der Vorspann ist identisch dem Heun-Verfahren.
# Runge-Kutta-Verfahren
:
# Hauptprogramm
dt=1 # Zeitschritt
t=0
while t<20:
print(t, v)
h0=h # kopieren, damit die Formeln
v0=v # symmetrisch sind
# mit Euler-Cauchy einen halben Schritt vorwärts
# h1 und v1 mit t, a0, v0 berechnen
a0=beschleunigung(t, v0, h0)
h1=h0+v0*dt/2
v1=v0+a0*dt/2
# h2 und v2 aus t+dt/2, a1, v1
a1=beschleunigung(t+dt/2, v1, h1)
h2=h0+v1*dt/2
v2=v0+a1*dt/2
# h3 und v3 aus t+dt/2, a2, v2
a2=beschleunigung(t+dt/2, v2, h2)
h3=h0+v2*dt
v3=v0+a2*dt
# Beschleunigung für das Ende des Intervalls bestimmen
a3=beschleunigung(t+dt, v3, h3)
# Taylor-Entwicklung, Polynom 2. Ordnung
h=h+dt*(v0+2*v1+2*v2+v3)/6
v=v+dt*(a0+2*a1+2*a2+a3)/6
t=t+dt
Es ist schwierig, im Vorhinein anzugeben,
welche Genauigkeit mit welcher Schrittweite erreicht wird. Sehr große
Schrittweiten können dazu führen, das das Verfahren aus dem Ruder läuft und
physikalisch unsinnige Ergebnisse liefert. Und was "sehr groß" ist, das hängt
vom Problem ab. Bei der Berechnung eines Mehrkörperproblems wie z.B. der
Planetenbewegung, kann es zu nahen Begegnungen von Körpern kommen. Wenn diese
mit zu großen Schrittweiten berechnet werden, dann werden die starken Kräfte
unverhältnismäßig weit in die Zukunft extrapoliert.
Insgesamt kann ich
empfehlen, eine Simulation nochmals mit einer halbierten Schrittweite
durchzuführen. Wenn die Ergebnisse vergleichbar sind, dann sind Schrittweiten
in diesem Bereich brauchbar. Der Vorteil von den vorgestellten Verfahren ist,
dass die Schrittweite in jedem Simulationszustand verkleinert oder auch
vergrößert werden kann. Wenn wie beim Mehrkörperproblem die physikalischen
Verhältnisse überschaubar sind, dann lässt sich recht einfach eine
Schrittweitensteuerung hinzufügen. Zeiten naher Begegnungen werden dann mit
geringerer Schrittweite durchlaufen.
Es ist prinzipiell möglich, Verfahren anzugeben, die mehr als vir Werte berechnen. Auf Grund dieser größeren Anzahl von Stützstellen lässt sich die Funktion im Einzelschritt durch ein Polynom höheren Grades annähern. Bei dieser Polynominterpolation neigen höher Ansätze zu Schwingungen und anderen numerischen Effekten. Wenn es nicht sehr gewichtige Gründe gibt, rate ich zum klassischen Runge-Kutta-Verfahren wie hier beschrieben.
Ich habe für das Beispiel der Lektion Differentialgleichungen benutzt: Den freien Fall mit Luftwiderstand. Ich habe Rechnungen mit allen drei Verfahren ausgeführt. Ausgewählt habe ich die Zeit t=4 s.
| Δt | v in m/s | (exakt: 26,352.211.124.909) | |
| Euler-Cauchy-Verfahren | Heun-Verfahren | Runge-Kutta-Verfahren | |
| 1 s | 28 | 26,2 | 26,351 |
| 0,1 s | 26,5 | 26,350 | 26,352.211.09 |
| 0,01 s | 26,37 | 26,352.1 | 26,352.211.124.909 |
| 1 ms | 26,353 | 26,352.210.9 | |
| 0,1 ms | 26,252.3 | 26,352.211.123 |
Uwe Pilz, Oktober 2019