A&A Title Image Startseite | Programm-Archiv | Algorithmus Euler-Cauchy-Verfahren | Unsere Vorläufer | Kontakt, Datenschutz

Das Euler-Cauchy-Verfahren zur numerischen Lösung von Differentialgleichungen

Das Verfahren in seiner einfachsten Form

Differentialgleichungen sind Funktionen, in denen neben den Unbekannten auch deren Ableitungen vorkommen. Ich habe dazu eine Einführung geschrieben, bitte diese zuerst lesen. Die formelmäßige Lösung, das Auffinden einer sog. Stammfunktion, gelingt in vielen Fällen nicht. Es gibt jedoch numerische Verfahren, welche eine Näherungslösung berechnen. Das einfachste und damit am leichtesten verständliche ist das Polygonzugverfahren nach Leonhard Euler und  Augustin-Louis Cauchy.

Das Verfahren eignet sich nicht für alle Arten von Differentialgleichungen. Insbesondere können sog. partielle Differentialgleichungen damit nicht gelöst werden – in diesen kommen Ableitungen nach mehreren Größen vor. Es ist aber gut geeignet für die in der Astronomie wichtigen Bewegungsanalyse und Bahnberechnung. Zunächst nehmen wir an:

All diese drei Einschränkungen lassen sich umgehen. Ich schreibe dazu weiter unten noch etwas.

Das Polygonzugverfahren ist simpel: Ausgehend vom Startwert berechnen wir die Ableitung, das ist der Anstieg der Kurve. Diese ist ja formelmäßig gegeben. In einer kleinen Umgebung des Startwertes wird sich diese Ableitung auch nur wenig ändern, zumindest bei gutmütigen Funktionen ohne Sprungstellen. Wir sehen daher diese Ableitung als gültig für einen kleinen Schritt in x-Richtung an, dieser kleine Schritt wird oft mit h bezeichnet. Der Anstieg führt vom Startpunkt (x0, y0) zum nächsten Punkt (x1, y1). Für diesen kann man wieder den Anstieg berechnen und zum Punkt (x2, y2) kommen usw.

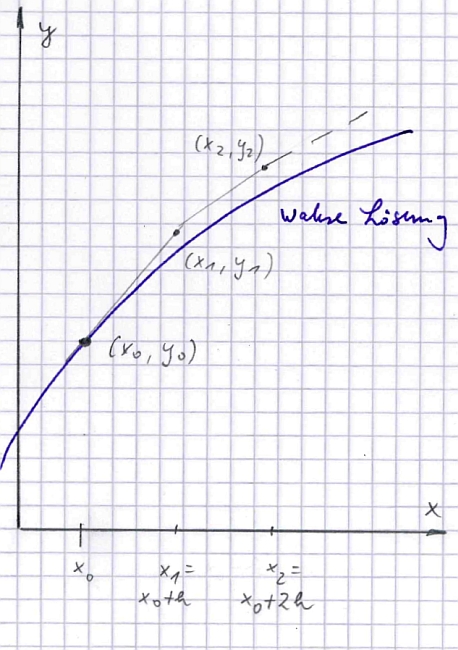
Die Abbildung macht ein Problem all dieser Näherungsverfahren deutlich: Jeder Rechenschritt erzeugt einen kleinen Fehler, der in den nächsten Schritt wieder eingeht: Die Fehler summieren sich. Man kann den Fehler verringern, in dem man die Schrittweite h verkleinert. Dies erhöht aber den Rechenaufwand und erzeugt auch irgendwann numerische Probleme. Andererseits besticht das Verfahren, weil es anschaulich ist und einfach programmierbar.

Die Ableitung ist nicht explizit gegeben

Es kann vorkommen, dass sich die Ableitung nicht isolieren lässt, weil sie an mehreren Stellen der Formel vorkommt. In solchen Fäller erfordert die Berechnung der Ableitung selbst ein Näherungsverfahren, z.B. das allgemeine Iterationsverfahren. Es ist jedoch unwichtig, wie aufwendige eine zumindest näherungsweise Berechnung der Ableitung ist: Wenn man sie irgendwie berechnen kann, dann lässt sich dieses Verfahren auch einsetzen.

Es treten höhere Ableitungen auf

In den Bewegungsgleichungen der Astronomie trten immer höhere Ableitungen auf. Neben dem Ort eines Körpers ist dessen Geschwindigkeit (die erste Ableitung des Ortes nach der Zeit) und die Beschleunigung in Flger der auf ihn wirkenden Kräfte (die zweite Ableitung des Ortes nach der Zeit) von Bedeutung. Solche Differentialgleichungen können gelöst werden, wenn man die eine Gleichung höherer Ordnung ein System von Gleichungen einfacher Ordnung umformt. Ich erläutere das an dem bereit bekannten Beispiel des Fallschirmspringers:

Das einzige, was wir zunächst wissen, ist die Kräftebilanz – die Gesamtkraft ist die Summe aus Erdanziehung und Luftwiderstand
        F = FG + FW
Die Gravitationskraft kann als konstant angenommen werden, FG = m · g . Der Luftwiderstand hängt ab von der Querschnittsfläche, der Geschwindigkeit und der Luftdichte. Die Querschnittsfläche und die Luftdichte werden in unserem Fall als konstant angesehen und durch eine Konstante β ausgedrückt. Die Widerstandkraft ist dann   FW = - β · v.

Wenn Ausgangsbedingungen gegeben sind:

dann kann man aus der Kräftebilanz die Beschleunigung berechnen, also die zweite Ableitung des Ortes (bei uns: der Höhe h) nach der Zeit:

h'' = [ FG(h) + FW(h') ] /m

Die Gewichtskraft ist hier eine Konstante, der Luftwiderstand hängt von der Geschwindigkeit ab. Gegeben und berechenbar ist also die Beschleunigung, unbekannt sind der Verlauf der Geschwindigkeit und der Höhe des Fallschirmspringers über die Zeit. Um nun das Euler-Cauchy-Verfahren (oder ein anderes, genaueres verfahren) einsetzen zu können, wird eine Hilfsvariable eingeführt, welche die erste Ableitung der Höhe enthält. In unserem Beispiel hat diese eine physikalische Bedeutung, es ist nämlich die Geschwindigkeit v.
Damit können wir aus der einen Gleichung mit einer Ableitung zweiten Grades zwei gekoppelte Gleichungen machen, welche nur noch Ableitungen ersten Grades enthalten. Des sind Anstiege, mit denen Polygone gezogen werden können:

 v' = FG/m + FW/m
h' = v

Für eine Differentialgleichung zweiter Ordnung benötigen wir auch zwei Anfangsbedingungen, nämlich eine Höhe h0 und eine Geschwindigkeit v0. Beide können wir zum Beispiel auf Null setzen. Das Polygonzugverfahren lässt sich jetzt wieder anwenden. Es wird ein Zeitschritt Δt festgelegt, dann berechnet man für jeden Schritt

  1. Die Beschleunigung für die aktuelle Zeit t
  2. die neue Geschwindigkeit für t+Δt aus der alten Geschwindigkeit und der Beschleunigung
  3. die neue Höhe für t+Δt aus dem alten Ort und der alten(!) Geschwindigkeit
  4. die neue Zeit durch Addition des Zeitschrittes Δt

Im Python-Programm habe ich zuerst die neue Höhe und dann die Geschwindigkeit berechnet, weil ich dadurch eine Hilfsvariable für die neue Geschwindigkeit eingespart habe. Wichtig für das Euler-Cauchy-Verfahren ist nur das Hauptprogramm. Es hat als Voraussetzung, dass sich die Beschleunigung prinzipiell berechnen lässt. 


# Euler-Cauchy-Verfahren
from math import *

# Konstanten
g=9.81
b=15

# Anfangsbedingungen
v0=0
h0=0
m=70

    
def beschleunigung(v): 
    a=g
    a=a-(b*v)/m
    return a


# Hauptprogramm
v=v0
h=h0 
dt=1     # Zeitschritt
t=0
while t<20:
    print(t, v)
    a=beschleunigung(v)
    h=h+v*dt 
    v=v+a*dt
    t=t+dt

Die Zeitschrittweite wurde mit 10 ms sehr kurz gewählt. Hiermit ergibt sich aber eine gute Genauigkeit und die vorhergesagte Endgeschwindigkeit von 45 m/s wird auch errechnet. Auch die Zeitkonstante stimmt:

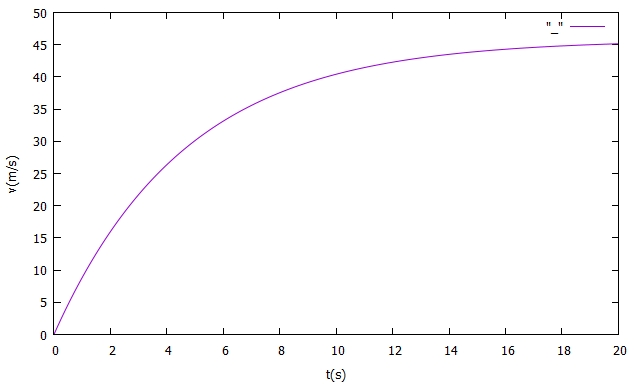
Ihr könnte mit dem Programm etwas experimentieren. Wenn man die Schrittweite zu kurz wählt, dann schwingen die Ergebnisse oder werden gar ganz unsinnig.Für wirkliche Anwendungen sind die Verfahren nach Karl Heun oder nach Carl Runge und Martin Wilhelm Kutta besser geeignet. Ich habe dazu einen eigenen Aufsatz verfasst.

Es sind Anfangs- und End-Bedingungen gegeben

Für eine Differentialgleichung zweiter Ordnung sind zwei Randbedingungen nötig. Im eben besprochenen Fall waren diese am Anfang des Rechenintervalls als sogenannte Anfangsbedingungen gegeben. Es ist aber auch möglich, dass die Bedingungen für das Ende des Rechenintervalls bekannt sind. Auch das ist kein Problem, dann rechnet man eben in der Zeit rückwärts. Schwierig wird es, wenn ein Teil der Bedingungen für den Anfang und ein Teil für das Ende gegeben wurden. Ein Beispiel: Ein Pilot verlässt das Flugzeug mit einem Schleudersitz, welcher ihn senkrecht nach oben schießt. Nach 5 Sekunden öffnet der Fallschirm. Zu diesem Zeitpunkt hat der Pilot eine Geschwindigkeit von 10 m/s. Wie hoch war die Anfangsgeschwindigkeit, die ihm der Schleudersitz verlieh?

Solche Fälle sind generell schwierig zu berechnen. Geeignet ist das sogenannte Schießverfahren. Der Begriff stammt aus dem sog. "Einschießen" der Artillerie, wo zunächst mit geschätzten Werten geschossen wird, das Ergebnis beobachtet und danach korrigiert. Man nimmt also irgendwelche Startwerte an, rechnet 5 Sekunden vorwärts und schaut auf das Ergebnis. Dann korrigiert man die Startwerte, bis man nahe genug am gewünschten Resultat ist.
Mit den heutigen schnellen Rechner kann man auch erwägen, für einige Dutzend Startgeschwindigkeiten ein Ergebnis zu berechnen, und aus der Tabelle der Ergebnisse das best geeignete herauszusuchen. Das geht aber nur, wenn die Rechnung in sich nicht allzu aufwendig ist.

Schießverfahren sind meist schlecht zu automatisieren.

(Uwe Pilz, Dezember 2018)