Einem Kind, das die Dunkelheit fürchtet, verzeiht man gern.
Tragisch wird es erst, wenn Männer das Licht fürchten.
Platon

Das Licht als Welle, eine Einführung

Manche Eigenschaften des Lichts lassen sich dadurch erklären, dass man es als sogenannte elektromagnetische Welle auffasst: Dies bedeutet, es gibt einen elektrischen Anteil E und einen magnetischen Anteil B, es schwingt und es bewegt sich im Raum fort.
Wir sehen allerdings weder den elektrischen noch den magnetischen Anteil, und diese lassen sich auch nicht ohne weiteres messen. Was wir sehen, ist die Intensität (die Helligkeit) und die Frequenz (die Farbe).

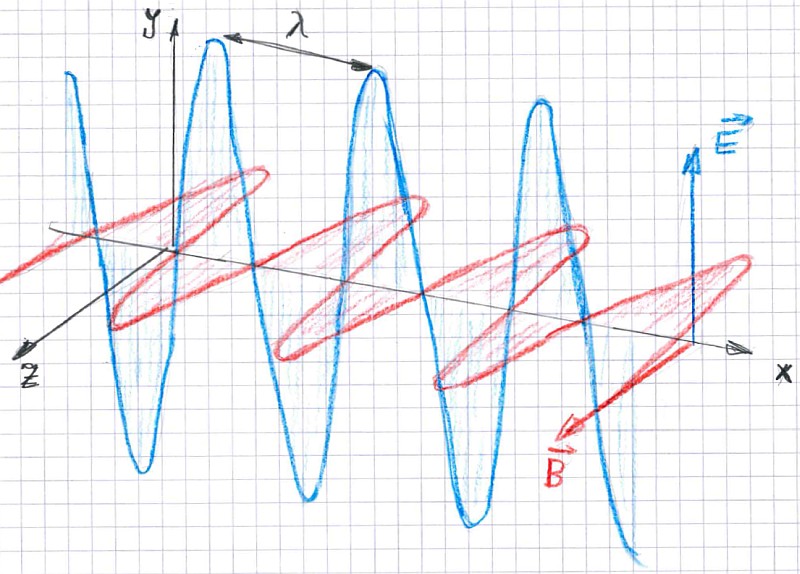
Wenn das Licht von einem kleinen Raumgebiet ausgeht, dann breitet es sich gleichmäßig nach allen Richtungen aus. Man spricht von einer Kugelwelle. Die Wellenfront ist also gekrümmt. Unter einer Wellenfront versteht man den Teil der Welle, welche den Sender zur selben Zeit verlassen haben.

Wenn der "Sender" (z.B. ein Stern) sehr weit entfernt ist, dann ist die Krümmung dieser Wellenfront sehr klein und nähert sich einer ebenen Welle an. Eine Ebene Welle hat nur eine Ausbreitungsrichtung (weg vom Sender), und man muss nur eine Koordinate betrachten. Und damit beginnen wir.

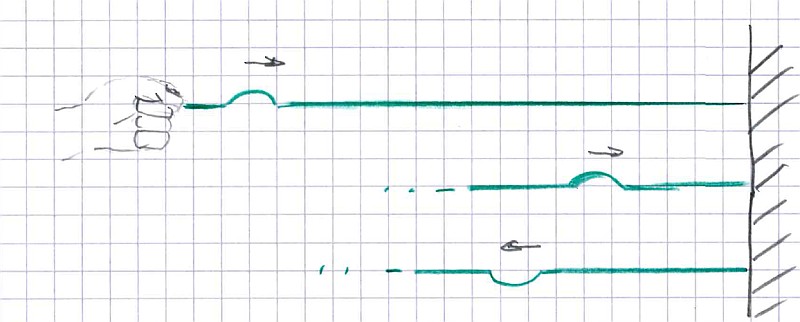
Leider kann man das Schwingen der Lichtwelle nicht sehen, und die Formeln sind unanschaulich. Zum Glück wird aber die Ausbreitung von Wellen in Saiten von Musikinstrumenten und auch in Seilen mit exakt denselben Gleichungen beschrieben. Dies ist viel anschaulicher. Fast jeder hat schon einmal eine Seilwelle erzeugt und vielleicht auch beobachtet, wie diese an einer Befestigung reflektiert wird:

Wieso wandert nun diese Welle am Seil entlang? Dazu muss man sich das Kräftediagramm an einem kurzen Seilstück ansehen. Dieses Seil sei mit der Kraft F0 gespannt. Wenn diese Kraft an einem Punkt in dieselbe Richtung zieht, dann gibt es keine Querkraft FQ, die eine Auslenkung bewirkt. Hierzu müssen die Kräfte links und rechts des Punktes unterschiedlich sein. Um das einfacher rechnen zu können, unterteilen wir das in x-Richtung laufende Seil in kurze Stücken Δx, für die wir die Kraft als konstant annehmen.

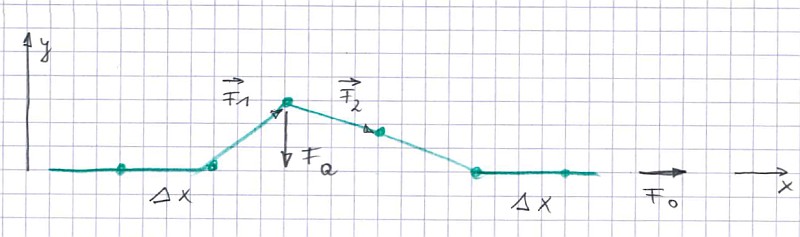
Die Kräfte F1 und F2 tragen Pfeile darüber, weil sie gerichtet sind. F0 und FQ sind zwar auch gerichtet, wir benötigen aber nur den Betrag. Von den beiden Teilkräften brauchen wir auch nur die y-Komponente, die sich aus rein geometrischen Erwägungen errechnen lässt. Für die Stelle x1:

F1,y = F0 · (y1 - y0 ) / Δx ; F2,y = F0 · (y2 - y1 ) / Δx

Mathematisch ist der Anstieg die Ableitung: Fy = F0 · dy/dx oder kürzer Fy =F0 · y' .

Die Rückstellkraft wiederum ist die Differenz der beiden Komponenten, wieder für die Stelle x1:

FQ = ( F2,y - F1,y ) bzw.
FQ = F0 /Δx · [( y2 - y1 ) - (y1 - y0 )]
FQ = F0 ( y2 - 2y1 - y0 ) /Δx

Nach der bekannten Formel F = m · a bewirkt diese Rückstellkraft die Beschleungung des Seilstücks. Dessen Masse errechnet sich aus der Länge des Seilstücks Δx und der linearen Dichte µ des Seils, gemessen in Kilogramm je Meter Seillänge. Es tritt an diesem Stück auch nur dier Kraftanteil Δx · FQ auf.

FQ = µ · Δx · a

oder anders geschrieben

FQ / Δx = µ · a

µ · a = F0 ( y2 - 2y1 - y0 ) /Δx²

Rechts steht damit die zweite Ableitung von y nach x, also y":

µ · a = F0 · y" bzw. a = F0 · y" / µ

Die Beschleungung a ist außerdem die zweite Zeitableitung in y-Richtung ÿ , die Punkte stehen für die Zeitableitung.

Zusammengefügt ergibt sich ÿ = F0 · y''/µ

Die Wurzel von F/µ hat die Einheit einer Geschwindigkeit. Dies ist übrigens die Ausbreitungsgeschwinidgkeit der Welle im Seil. Wir bezeichnen dies mit c, im Unterschied zur Quer-Geschwindigkeit v eines Seilstücks.

Somit ergibt sich

ÿ = c² · y''

Diese Differntialgleichung ist völlig identisch zu derjenigen einer Feldkomponente (E oder B) des elektrogamnetischen Feldes und damit des Lichts. c ist dann die Lichtgeschwindigkeit, die sich jedoch aus anderen Materialkonstanten zusammensetzt.

Es ist uns also möglich, ein kleines Programm zu schreiben, was mit mechnischen Größen hantiert und damit anschaulich ist. Die Ergebnisse dieses Programms lassen sich unverändet auf ebene Wellen übertragen!

--> 1 Einführung
--> 2 Funktionsweise des Programms
--> 3 Rechenergebnisse
--> 4 Sinuswelle
--> 5 Das Soliton
--> 6 Die Kugelwelle
--> 7 Interferenz zweier Wellenzüge (Formel)

Uwe Pilz, November 2020