Insofern sich die Sätze der Mathematik
auf die Wirklichkeit beziehen,
sind sie nicht sicher,
und insofern sie sicher sind,
beziehen sie sich nicht auf die Wirklichkeit.
Albert Einstein

Interferenz zweier Wellenzüge

Wellenzüge gleicher Amplitude

Die schillernden Farben bei Seifenblasen und Ölfilmen auf Wasser entstehen durch die Überlagerung (Interferenz) von Wellenzügen. In den vorigen Teilen haben wir experimentell ermittelt, dass man Kosinus-Funktionen für solche Überlagerungen benutzen kann, anstatt die Wellengleichung numerisch auszurechnen. Besonders einfach wird dies, wenn wir annehmen, dass die Amplituden der beiden Wellenzüge gleich groß sind. Viele technische Anwendungen (z.B. Antireflexschichten auf Optiken) werden so bemessen, dass gerade dieser Fall eintritt.

Elektromagnetische Wellen bestehen aus zwei Komponenten, einer magnetischen und einer elektrischen. Die gemessene und wahrnehmbare Intensität ist das Produkt der beiden und damit proportional zum Quadrat einer der beiden Komponenten. Ich verwende hier die Auslenkung u als Stellvertreter einer der beiden Beiträge.

Es sollen sich Wellenzüge überlagern, die um den Betrag δ verschoben sind. Ich habe sie mit u₁ und u₂ bezeichnet:

u₁ = A cos [ 2π ( x/λ -t/T)]
u₂ = A cos [ 2π ( (x-δ)/λ -t/T)]

u = u₁+ u₂ = 2A cos ( 2πδ/2λ) cos [ 2π (x/λ -t/T- δ/2λ)]
Um dies nachzurechnen, benötigt man ein Additionstheorem für Winkelfunktionen:
cos α + cos β = 2 cos [ (α+β)/2] cos [ (α-β)/2]

Diese Formel für u hat einen festen Vorfaktor f, der nur von der Verschiebung δ abhängt:
f = 2A cos (πδ/λ) .

Die Intensität I ermittelt man, in dem man das Quadrat von u (Quadrat wegen der beiden Komponenten E und B) zeitlich mittelt:

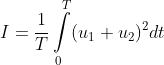
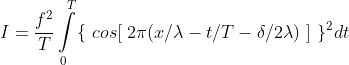
Das Integral vom Quadrat eines Wellenzuges hat den Wert 1/2, so lange ganze Perioden berücksichtigt werden. Ich habe das mit Hilfe von χCas ausgerechnet.

I = 2A² [cos(πδ/λ)]²

Wenn man die Verschiebung der Wellenzüge in Einheiten der Wellenlänge angibt, dann wird es noch einfacher:

I = 2A² [cos(πδ)]²

Ich habe ein kleines Programm geschrieben, mit welchem man sich dies veranschaulichen kann. Es zeichnet den Verlauf der Amplitude u in rot und den des Quadrates der Amplitude in blau. Man erkennt:

- der x-Wert führt lediglich zur Verschiebung des Wellenzuges. Man kann also auch mit x=0 rechnen
- eine Verschiebung um δ = λ/2 führt zur Auslöschung des Wellenzuges

Außerdem wird die Intensität durch numerische Integration der Einzelbeiträge u² und schließlich durch die Formel angegeben, wobei ich die Amplitude A im Programm zu 1 setze. Hier ein Beispiel für x=0,1 und δ = 0,9:

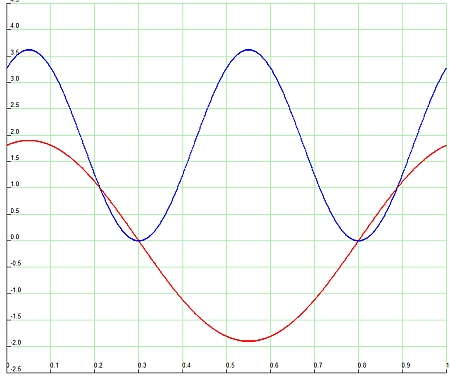
numerisch: 1.8090169943749503 analytisch: 1.8090169943749472

Und nun noch das Programm. Es erfordert wieder das Modul plot.py im selben Verzeichnis.


# Interferenz zweiter Cos-Wellen, Amplitude und Intensität

from math import *
from turtle import *
from random import *
from plot import *
import sys

def sq(x):
    return x * x
 
# Main
initKoor(0,1,0.1,-2.5,4.5,0.5)
x=0.1 # x in Einheiten von Lambda
t=0 # t in Einheiten der Periode T
dt=1/1000
delta=0.9 #in Einheiten von Lambda
I=0
while t<1:
    u=cos(2*pi*(x-t))+cos(2*pi*(x+delta-t))
    Plot(t,u,3,"red")
    Plot(t,u*u,3,"blue") # Intensität
    t=t+dt
    I=I+u*u*dt
update()
hideturtle()
print ("numerisch: ", I, "analytisch: ", 2*sq(cos(pi*delta)))
name = input("ENDE!")

Wellenzüge unterschiedlicher Amplitude

Es sollen sich Wellenzüge überlagern, die um den Betrag δ₀ verschoben sind und die Amplituden A₁ und A₂ aufweisen. Ich habe sie wieder mit u₁ und u₂ bezeichnet:

u₁ = A₁ cos [ 2π ( x/λ -t/T)]
u₂ = A₂ cos [ 2π ( (x-δ)/λ -t/T)]

Zunächst berechnet man die resultierende Amplitude A und die resultierende Phasenverschiebung δ

φ₀= 2π δ₀/ λ
A² = A₁² + A₂² + 2 · A₁ · A₂ · cos φ₀
tan φ = ( A₂ · sin φ₀) / ( A₁ + A₂ · cos φ₀)
δ = φλ/(2π)

Die vereinte Welle u ist dann

u = u₁+ u₂ = A cos [ 2π ( (x-δ)/λ -t/T)]

Die Intensität I ermittelt man, in dem man das Quadrat von u (Quadrat wegen der beiden Komponenten E und B) zeitlich mittelt:

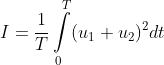
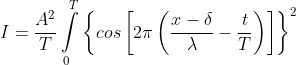
Das Integral hat wieder den Wert 1/2. Es ergibt sich

I = A² /2

Ich habe wiederein kleines Programm für Experimente geschrieben. Man kann zwei Amplituden eingeben und es gibt eine Grafik für alle Verschiebungen δ₀ von 0 bis T=1.


# Interferenz zweiter Cos-Wellen unterschiedlicher Amplitude: Berechnung der
# Intensität
from math import *
from turtle import *
from random import *
from plot import *
import sys

# Main
um = 1e-6 # Mikrometer
T = 1
L = 0.55 * um
A1 = 1
A2 = 0.5
d0 = 0
dd = L / 100

initKoor(0,1,0.1,0,4,0.5)
while d0 < L:
    phi0 = 2 * pi * d0 / L
    A = sqrt(A1 * A1 + A2 * A2 + 2 * A1 * A2 * cos(phi0))
    tanF = (A1 * sin(0) + A2 * sin(phi0)) / (A1 * cos(0) + A2 * cos(phi0))
    phi = atan(tanF)
    d = phi * L / (2 * pi)
    Plot(d0 / L, 0.5 * A * A , 3, "magenta")
    d0 = d0 + dd
    update()
hideturtle()
name = input("ENDE!")

--> 1 Einführung
--> 2 Funktionsweise des Programms
--> 3 Rechenergebnisse
--> 4 Sinuswelle
--> 5 Das Soliton
--> 6 Die Kugelwelle
--> 7 Interferenz zweier Wellenzüge (Formel)

Uwe Pilz, Januar 2021