Die Worte verbinden nur,
wo unsere Wellenlängen längst übereinstimmen.
Max Frisch

Licht als Welle – Sinuswelle

Die Beispiele des ersten Teils gaben "unsaubere" Ergebnisse. Wenn man sich dies nicht als Seil, sondern als Gitarrensaite vorstellt, dann würde diese nicht rein klingen, sondern klirren. Der Grund dafür ist die sog. Dispersion, d.h. das Zerfließen der ursprünglichen Auslenkungen auf einen größeren Bereich, schließlich übergreifend auf das gesamte Seile / die gesamte Saite.

In diesem Teil möchte ich näher an die Lichtwellen herankommen. Das Rechenprogramm ist praktisch gleich: Das ist ja erlaubt, weil die Differentialgleichungen identisch sind. Allerdings habe ich die Programmvariablen teilweise umgenannt, um näher an die physikalische Beschreibung elektromagnetischer Wellen zu kommen.

In diesem Programm gibt es eine Anregung auf der linken Seite. In Abhängigkeit davon, wie diese Anregung erfolgt, ergeben sich verschiedene Muster. Die meist dargestellte Lösung einer Wellengleichung ist die in diesem Teil vorgestellte kontinuierliche Sinuswelle. Es gibt aber noch andere Lösungen, von denen ich einige im nächsten Teil vorrechnen werden.

Anregungen, welche mit der Wellengleichung verträglich sind, bilden ein Muster, was sich im Raum fortbewegt, dabei aber nicht verändert. Andere Anregungen führen zur Veränderung des Musters, zum räumlichen Zerfließen (Dispersion).

Eine kontinuierliche Sinuswelle entsteht, wenn am Rand des Gebietes (bei uns links) das Ende in einem Sinusrhythmus bewegt wird. Eine elektromagnetische Welle (Licht ist eine solche) besteht aus einem elektrischen Anteil E und einem magnetischen Anteil B. Diese beiden Größen sind gleichlaufend. Ich gebe hier die Formeln für E, was jetzt anstelle der Seilauslenkung Y benutzt wird. Für die Sinuswelle gilt als Erregung

E(x=0, t) = E_max sin ( 2 π (t/T) )

Hier ist T eine Periodendauer. Die Welle schreitet mit der Geschwindigkeit c voran, hieraus ergibt sich die Wellenlänge λ:

λ = c · T

Nach einer Weile sieht das so aus:

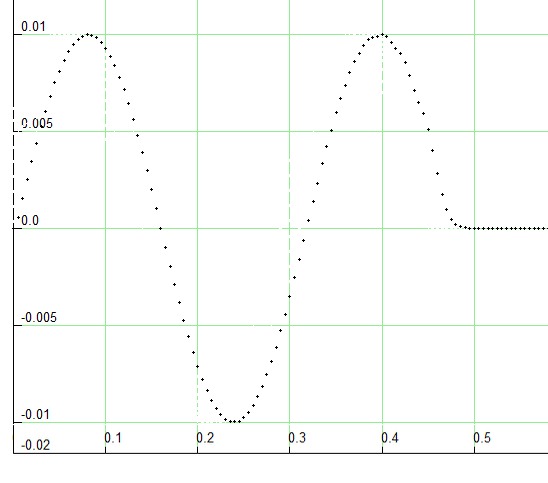
Die Schwingung an jedem Ort wird auch durch die obige Gleichung beschrieben, mit einem zusätzlichen Zeitversatz. Das heißt, nachdem die anfängliche Wellenfront vorbeiglaufen ist, schwingt jeder Punkt im Sinusrhythmus. Zum Vergleich zeigt eine einzelne kurze Störung (ein Impusl) am Anfang deutliche Dispersion:

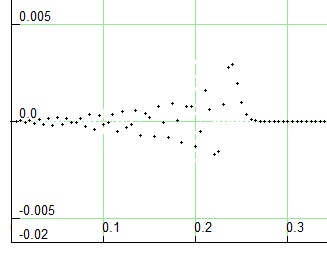
Mit kleinen Experimenten der Anregung kann man also feststellen, ob die Wellengleichung durch eine bestimmte Art der Anregung zumindest näherungsweise erfüllt wird. Für die Sinuswelle scheint das der Fall zu sein, für eine einzelne Auslenkung am Anfang nicht.

Da die Form der Sinuswelle also erhalten bleibt, wenn sich diese aber im Raum fortbewegt, kann man eine vollständige Gleichung angeben-. Diese beschreibt sowohl das zeitliche Verhalten, als auch die räumliche Ausbreitung. Es sei daran erinnert, dass ich hier ebene Wellen betrachten, die sich nur in eine Richtung ausbreiten. Solche Wellen ergeben sich näherungsweise bei sehr weit entfernten punktförmigen Lichtquellen.

Die vollständige Gleichung:

E(x, t) = E_max sin ( 2 π (t/T - x/λ ) )

Es ist viel praktischer, mit dieser Gleichung zu rechnen, an statt wie hier die Differentialgleichung jedes Mal zu sumulieren.

Wie im ersten Teil gezeigt, lassen überlagern sich Wellen, ohne sich gegenseitig zu beeinflussen. Wenn man diese Erkenntnis hinzunimmt, dann kann man schon recht komplexe Fragestellungen der Wellenoptik simulieren – einfach durch Sinusfunktionen. Bei einer solchen Überlagerung muss man beachten, dass die verschiedennen Wellenzüge nicht gleichlaufend sein müssen, sondern eine Phasenverschiebung φ haben können. Die müssen wir noch hinzunehmen, dann haben wir alles.

E(x, t) = E_max sin ( 2 π (t/T - x/λ ) + φ )

Wenn man das Differenzieren beherrscht, dann kann man kann nachrechnen, dass die Wellengleichung

c · δ²E/δx² = δ²E/δt²

erfüllt ist. Ich gebe hier eine Lösung, die ich mit dem Computeralgebrasystem χCas berechnet habe .

Das Programm zur Simulation liegt im Archiv. Hier gibt es wieder verschiedene Modi, mit denen man experimentieren kann. Die Sinuswelle ist Modus 2, die oben gezeigte Störung ist Modus 0.

--> 1 Einführung
--> 2 Funktionsweise des Programms
--> 3 Rechenergebnisse
--> 4 Sinuswelle
--> 5 Das Soliton
--> 6 Die Kugelwelle
--> 7 Interferenz zweier Wellenzüge (Formel)

Uwe Pilz, Dezember 2020