Mich erstaunen Leute, die das Universum begreifen wollen,
wo es schwierig genug ist,in Chinatown zurechtzukommen.
Woody Allen

Licht als Welle – das Soliton

Die Welt um uns herum ist voller wunderbarer Erscheinungen, wir müssen nur hinschauen. Mich faszinieren die Einzelwellen, die sich über riesiege Entfernungen fortbewegen, ohne ihre Form zu verändern, also ohne abzuflachen und Energie zu verlieren. Sie werden Solitone genannt. Im Meer treten als sie Riesenwelle (Kawentsmann) oder Tsunamiwelle auf.

Auch mit unserem Seil-Experiment kann man solche Solitonen nachstellen. Es gibt verschiedene Varianten. Die einfachste kann mit der Anregung

E(x=0, t) = E_max / (e^-t/T+ e ^t/T)

erzeugt werden. Das Programm im Archiv enthält dieses Soliton im Modus 5.

Ich verwende gleich wieder die elektrische Feldstärke der elektromagnetischen Welle. T ist hier keine Periode, sondern ein Wert, der den zeitlichen Verlauf und damit die räumliche Ausdehnung verändert, die Welle also schmaler oder breiter macht. Um so etwas zu erzeugen, kann man nun nicht bei t=0 anfangen, sondern muss zu einem Zeitpunkt beginnen, bei dem die Amplitude sehr klein ist. Im Programm habe ich das durch eine Verschiebung der t-Achse realisiert.

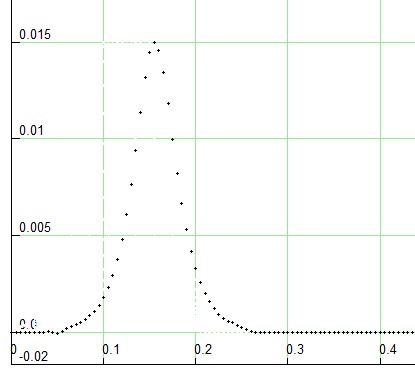
Diese Welle läuft ohne die Form zu verändern das Seil entlang, auch das Experiment zeigt keine Dispersion. Ich habe nachgerechnet, dass die Funktion die Wellengleichung erfüllt.

Vielleicht helfen die Solitonen für die Vorstellung der Ausbreitung des Lichts. Einerseits wird den Photonen Wellencharkter zugeschrieben, andereseit breiten sie sich nicht wie Wellen aus, also nicht kugelförmig im Raum. Vielleicht sind Photonen auch eine Art Solitärwelle? Zumindest sind sie es nicht im Sinne der hier zugrundeliegenden Maxwellschen Gleichungen.

Solche Wellen-Formeln müssen wären komplizierter sein, weil sie nicht nur in einer Dimension durch die eigene Struktur zusammengehalten werden müssen, sondern sozusagen allseitig.

Außerdem haben Photonen eine Frequenz, ein Soliton aber nicht. Diesen Effekt können wir mit unseren Experimenten nachstellen, in dem man die Solitonwelle mit einer Sinusfunktion überlagert:

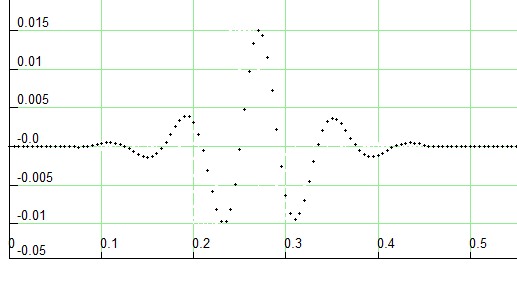
Die Anregung ist:

E(x=0, t) = cos (z · t/T) E_max / (e^-t/T+ e ^t/T)

Der Wert z gibt an, wie dicht die Schwingungen liegen. Zum selbst nachrechnen: Modus 6 im Programm.

Ich habe auch hierfür nachgerechnet, dass die Wellengleichung erfüllt ist.

Vergleich mit dem Dirac-Impuls

Ich habe in der vorigen Folge den Dirac-Impuls vorgestellt, eine kurzzeiteige "Störung". Man kann sich diesen durch eine unendlich schmale, aber unendlich hohes Rechteck mit der Fläche 1 vorstellen. Ein solches Rechteck hat mathematisch den cähnlich verhalten, aber differenzierbar sind. Ich habe mit

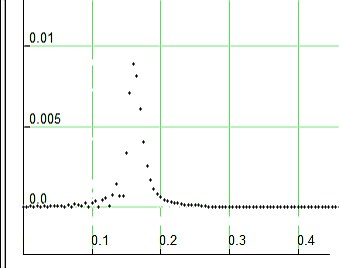
E(x=0, t) = E_max σ/ (σ + t²)

experimentiert:

Je kleiner der Wert von σ, desto schmaler wird der Impuls. Für das Beispiel habe ich einen recht breiten Impusl gewählt.

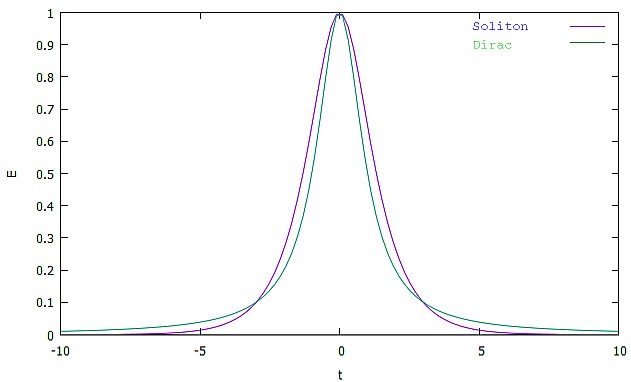
Die Wellengleichung für den Dirac-Impuls ist nicht erfüllt, und er erzeugt Dispersion, ganz ähnlich derjenigen der Rechteckfläche im vorigen Teil:

Interessant ist, dass die beiden Funktionen recht ähnlich sind, wenn man sie geeignet skaliert.

--> 1 Einführung
--> 2 Funktionsweise des Programms
--> 3 Rechenergebnisse
--> 4 Sinuswelle
--> 5 Das Soliton
--> 6 Die Kugelwelle
--> 7 Interferenz zweier Wellenzüge (Formel)

Uwe Pilz, Dezember 2020