Wissenschaft kann die letzten Rätsel der Natur nicht lösen.
Sie kann es deswegen nicht, weil wir selbst ein Teil der Natur
und damit auch ein Teil des Rätsels sind, das wir lösen wollen.
Max Planck

Licht als Welle – die Kugelwelle

Im ersten Teil haben wir die Seilwelle als Ausgangspunkt genommen. Eine solche Welle hat nur eine Ausbreitungsrichtung, entlang des Seils. Die Differentialgleichung war deshalb recht einfach:

δ²E/δt² = c² · δ²E/δx² oder noch kürzer

Ë = c² · E''

Eine elektromagnetische Welle bewegt sich jedoch im Raum, also in allen drei Koordinaten. Die Seilwelle ließ sich nur anwenden, weil wir auf eine ebene Welle eingeschränkt haben, bei der Änderungen nur in einer Richtung, eben der Ausbreitungsrichtung vorkommen. Im allgemeinen Fall muss man alle drei Koordinaten berücksichtigen:

δ²E/δt² = c² · ( δ²E/δx² + δ²E/δy² + δ²E/δz²)

Eine Kugelwelle beschreibt man am besten mit Kugelkoordinaten:

x = r · cos(φ) · sin(θ)
y = r · sin(φ) · sin(θ)
z = r · cos(θ)

Dieselbe Feldstärke E hat in Kugelkoordinaten natürlich eine andere formelmäßige Darstellung, die ich mit È bezeichne. Den Übergang von kartesischen zu Kugelkoordinaten ergibt eine recht aufwendige Rechnung

δ²E/δx² + δ²E/δy² + δ²E/δz² = δ²È/δr² + (2/r) · δÈ/δr² + (1/r²) · Δ_wÈ

Der Ausdruck Δ_wÈ stellt dabei die recht komplizierte Ableitung der Feldstärke nach den Winkeln φ und θ dar. Wir betrachen hier nur kugelsymmetrische Wellen, für welche dieser Operator 0 ist. Die Differentialgleichung ist dann

δ²E/δt² = c² · δ²È/δr² + (2/r) · δÈ/δr²

Um den Faktor 2/r zu berücksichtigen, kann man es mit dem Ansatz

È(r, t) = (1/r) · f(r + c·t)

versuchen.

Im Vergleich dazu kann die ebene Welle aus dem Ansatz

E(x, t) = f(x + c·t)

hergeleitet werden.

Damit ergibt sich: Alle Lösungen, welche für die ebene Welle gültig sind, können auch für die Kugelwelle verwendet werden, wenn man sie durch r dividiert. Die Feldstärke nimmt linear mit dem Radius ab.

Dies scheint zunächst der Erkenntnis zu wiedersprechen, dass die Intensität quadratisch mi dem Radius abnimmt. Hierbei muss man beachten, dass die Intensität das Produkt aus elektrischem und magnetischen Anteil der eletromagnetischen Welle sind. Beide sind gleichlaufen, hier noch einmal die Skizze:

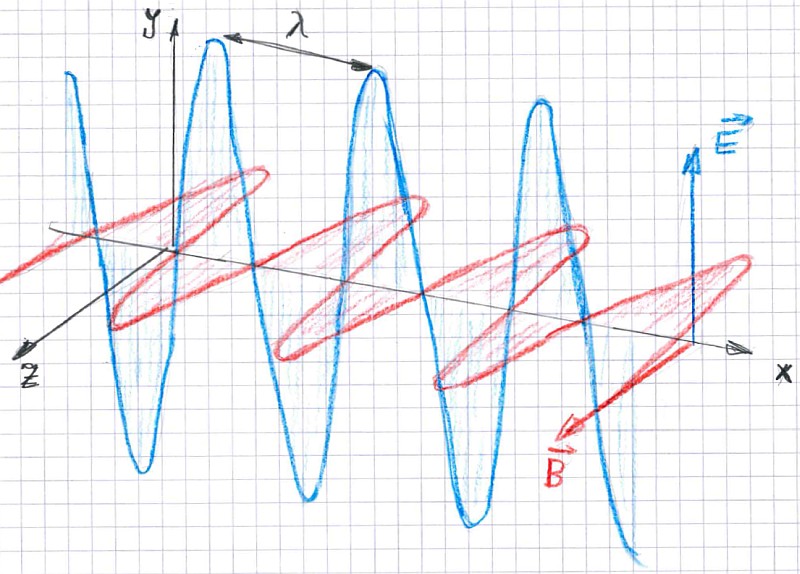
Damit nimmt das Produkt der beiden mit 1/r² ab.

Diese Erläuterungen und Berechnungen führen zum Resultat, dass wir berechtigt sind, sowohl ebene als auch Kugelwellen durch Sinus- oder Kosinusfunktionen zu beschreiben. Es wird damit unnötig, die rechenzeit-aufwendige schrittweise räumliche und zeitlich Summation bzw. Integration auszuführen.

--> 1 Einführung
--> 2 Funktionsweise des Programms
--> 3 Rechenergebnisse
--> 4 Sinuswelle
--> 5 Das Soliton
--> 6 Die Kugelwelle
--> 7 Interferenz zweier Wellenzüge (Formel)

Uwe Pilz, Januar 2021